Research Article - Journal of Applied Mathematics and Statistical Applications (2018) Volume 1, Issue 2
Which one shall we use for linear dynamic panel models: GMM or IV?
- *Corresponding Author:
- Yonghui Zhang
Department of Economics Renmin University of China 59 Zhong- Guancun Road, Beijing, 100872, P.R.China
Tel: 010 8250 0732
E-mail: yonghui.zhang@hotmail.com
Accepted date: June 20, 2018
Citation: Zhang Y, Zhou Q. Which one shall we use for linear dynamic panel models: GMM or IV? J Appl Math Stat App. 2018;2(1):1-4.
Abstract
In this paper, we consider the estimation of dynamic panel data models. We establish the equivalence of the GMM estimator proposed by Alvarez and Arellano, which is based on the forward differenced model using all lagged variables as instruments, and the double filter instrumental variables estimator (DIV for short) proposed by Hayakawa, which uses the backward differenced lags as instruments. Since the DIV estimator is asymptotically unbiased, thus we suggest using the DIV estimator for estimation of dynamic panel models. Monte Carlo simulations confirm our findings in this paper.
Keywords
Dynamic panel data model, Generalized method of moments, Instrumental variable estimation, Forward demeaning, Asymptotic efficiency.
JEL Classification: C01, C13, C23
Introduction
One of the unique features of the dynamic panel models is the presence of unobserved individual- specific effects creates the correlation between all past, current and future observations [1-3]. However, since the individual-specific effects appears linearly in the model, in principle, any differencing method that preserves the linear structure of the model can eliminate the time- invariant individual-specific effects. After elimination of individual-specific effects, another unique feature of dynamic panel model is that lagged dependent variables can be used to construct orthogonal conditions. As a result, either generalized method of moments (GMM) or instrumental variables (IV) method can be adopted to estimate the unknown parameters. As pointed out by Blundell et al. [4], GMM estimator is in general more efficient than the IV estimator for linear dynamic panel models. It is also shown by Alvarez and Arellano [1] that the GMM estimator based on forward differenced model using all lagged variables as instruments attains the asymptotic efficiency bound when the normality is assumed with regard to the errors. However, for the double filter instrumental variables (DIV) estimator recently proposed by Hayakawa [2] and Hayakawa et al. [5], it also reaches the asymptotic efficiency bound for dynamic panels. In order to understand the connection of these two estimators, we discuss the equivalence between these two estimators in this paper. We show that the GMM estimator and the DIV estimator are asymptotically equivalent in the large dynamic panel models. Since the DIV estimator is asymptotically unbiased, thus we suggest using the DIV estimator for estimation of dynamic panel models. Monte Carlo simulations are provided to examine the finite sample properties of these estimators. Section 2 sets up the basic model and the estimators of interests, equivalence between the estimators are also discussed in this section. Results of Monte Carlo studies illustrating the finite sample properties are presented in section 3. Concluding remarks are in section 4.
Materials and Methods
Model
In this paper, we consider the simple linear dynamic panel model of the form
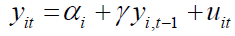 . (2.1)
. (2.1)
For the above model, we assume that
Assumption 1 (A1):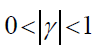
Assumption 2 (A2): 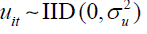 over i and t with finite
fourth-order moment.
over i and t with finite
fourth-order moment.
Assumption 3 (A3): {αi} are ΙΙD over i with 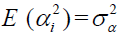 and finite fourth-order moment and independent of
and finite fourth-order moment and independent of 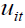 .
.
Assumption 4 (A4): The initial condition yi0 follows the stationary distribution
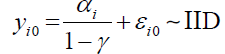
where 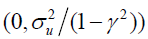 .
.
The above assumptions are quite standard for dynamic panel models in the literature, e.g., Alvarez and Arellano [1] and Hsiao and Zhou [6].
GMM and DIV estimation
For model (2.1), as discussed before, the unobserved individualspecific
effects 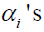 create the serial correlation between yit
and yis for all t ≠ s. Any differencing method that preserves the linear structure of (2.1) can eliminate the time-invariant αi ; for instance, see the first difference (FD) by Anderson and Hsiao
[7,8] and Arellano and Bond [9] and the forward demeaning
(FOD) by Arellano and Bover [10] and Alvarez and Arellano
[1]. However, the transformed regressors in the differenced
model are usually endogenous and the IV or GMM approach
are frequently adopted to estimate the unknown parameters. In
this paper, we focus on the method of FOD.
create the serial correlation between yit
and yis for all t ≠ s. Any differencing method that preserves the linear structure of (2.1) can eliminate the time-invariant αi ; for instance, see the first difference (FD) by Anderson and Hsiao
[7,8] and Arellano and Bond [9] and the forward demeaning
(FOD) by Arellano and Bover [10] and Alvarez and Arellano
[1]. However, the transformed regressors in the differenced
model are usually endogenous and the IV or GMM approach
are frequently adopted to estimate the unknown parameters. In
this paper, we focus on the method of FOD.
For model (2.1), the forward differenced model is given by
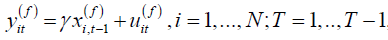 , (2.2)
, (2.2)
where
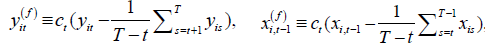 , and
, and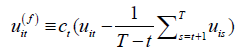 with
with 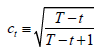 . Note
that in the transformed model (2.2)
. Note
that in the transformed model (2.2) 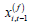 is endogenous because
of
is endogenous because
of 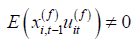 . Under Assumptions A2-A3, we have the
moment conditions
. Under Assumptions A2-A3, we have the
moment conditions
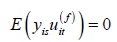 for all s < t , (2.3)
for all s < t , (2.3)
which imply that all the lagged dependent variables for the t
th time period can be used as the instruments for endogenous
regressor 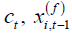 . The vector form of (2.2) is given by
. The vector form of (2.2) is given by
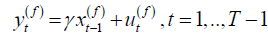 , (2.4)
, (2.4)
where 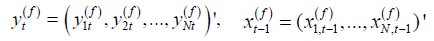 and
and 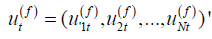 .
.
The GMM estimator (Alvarez and Arellano [1]) of γ based on (2.4) and the moment conditions (2.3) is given by
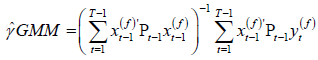 , (2.5)
, (2.5)
where 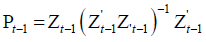 with
with
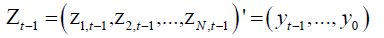 being the N ×t matrix of instruments. Clearly,
being the N ×t matrix of instruments. Clearly, 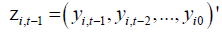 is the (t −1) instrumental variables
for
is the (t −1) instrumental variables
for 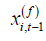 Under Assumptions A1-A4, it has been shown by
Alvarez and Arellano [1] that
Under Assumptions A1-A4, it has been shown by
Alvarez and Arellano [1] that
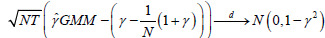 . (2.6)
. (2.6)
as (N,T )→∞, and γˆGMM attains the asymptotic efficiency
bound for linear dynamic panel models when '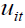 's follow
normal distribution.
's follow
normal distribution.
Alternatively, Hayakawa [2] and Hayakawa et al. [5] propose an estimator called double filter instrumental variable (DIV) estimator for the linear dynamic panel data models.
Let 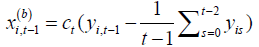 for i =1,..., N and
t =1,...,T. By Assumptions 2-3, it is obvious that
for i =1,..., N and
t =1,...,T. By Assumptions 2-3, it is obvious that
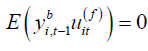 . (2.7)
. (2.7)
since 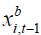 is a linear combination of all realized observations
at time (t −1) while
is a linear combination of all realized observations
at time (t −1) while 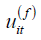 it contains all future errors from time t. The double filter instrumental variable estimator is just the
simple IV estimator
it contains all future errors from time t. The double filter instrumental variable estimator is just the
simple IV estimator
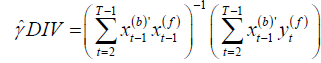 (2.8)
(2.8)
where 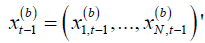 . Under Assumptions A1-A4,
it is shown by Hayakawa [7] and Hayakawa et al. [5] that
. Under Assumptions A1-A4,
it is shown by Hayakawa [7] and Hayakawa et al. [5] that
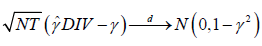 , (2.9)
, (2.9)
which suggests the DIV estimator (2.8) also attains the asymptotic efficiency bound for linear dynamic panel models when the errors are normally distributed.
Equivalence between the GMM and DIV estimators
In the above sections, we notice that both the GMM and DIV estimators attain the asymptotic efficiency bound for linear dynamic panel models. In this section, we establish the equivalence between the GMM and DIV estimators.
For the GMM estimator, let 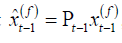 , then we have
, then we have
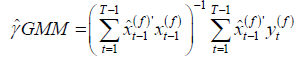 , (2.10)
, (2.10)
where 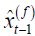 is the linear projection of yt −1 on the instruments
matrix Zt −1 , Thus the GMM estimator can be viewed as an
(optimal) IV estimator which utilizes
is the linear projection of yt −1 on the instruments
matrix Zt −1 , Thus the GMM estimator can be viewed as an
(optimal) IV estimator which utilizes 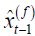 as instruments.
The equivalence between the GMM and DIV estimators is
summarized in the following proposition.
as instruments.
The equivalence between the GMM and DIV estimators is
summarized in the following proposition.
Remark 2.1: For model (2.1), if forward demeaning is utilized
to eliminate the individual- specific effects, and assume 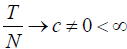 as both (N,T )→∞, then the GMM estimator
(2.5) is asymptotically equivalent to the DIV estimator (2.8), i.e.,
as both (N,T )→∞, then the GMM estimator
(2.5) is asymptotically equivalent to the DIV estimator (2.8), i.e.,
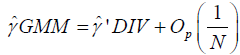 . (2.11)
. (2.11)
Proof of the proposition is provided in the appendix.
Remark 2.2: From the above proposition, we note that even if the GMM estimator uses all lagged variables as instruments in the estimation, it is asymptotically equivalent to the double IV estimator. For the double IV estimator, even if it is called IV estimator, but the instruments used in the estimation is totally different from the usual simple IV estimation (Hsiao and Zhou [6]), since the double IV uses the linear combination of all lagged variables as instruments, while the simple IV only uses one lagged variable as instrument. As shown by Hsiao and Zhou [6], the simple IV estimator is not as efficient as the GMM or DIV estimator for linear dynamic panel models.
Remark 2.3: The choice of GMM or DIV estimator depends on
the trade-off of efficiency and bias. It is shown by Alvarez and
Arellano [1], that, even if the GMM estimator is consistent, but it
is asymptotically biased of order 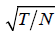 . However, for the DIV
estimator, it is shown by Hayakawa [2] and Hayakawa et al. [5]
that it is asymptotically unbiased. Since the DIV estimator also reaches the asymptotic efficiency bound, then we can conclude
that the DIV estimator is a preferable choice for estimation of
dynamic panel models in terms of unbiasedness and asymptotic
efficiency.
. However, for the DIV
estimator, it is shown by Hayakawa [2] and Hayakawa et al. [5]
that it is asymptotically unbiased. Since the DIV estimator also reaches the asymptotic efficiency bound, then we can conclude
that the DIV estimator is a preferable choice for estimation of
dynamic panel models in terms of unbiasedness and asymptotic
efficiency.
Remark 2.4: The mathematical equivalence between GMM and FOD is based on both N and T are large, however, for empirical practice, it is usually assumed T is small. In such a scenario, it is obvious that the GMM estimator is asymptotically more efficient than the DIV estimator. This is because the moment condition (2.7) is based on backward-demeaning, which can be represented as a linear combination of the instruments employed by the GMM estimator. The efficiency gap between GMM and DIV disappears as T tends to infinity.
Result and Discussion
In this section, we investigate the finite sample properties for GMM, DIV as well as simple IV estimation of γ for dynamic panel model. We consider the following data generating process (DGP)
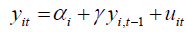 .
.
we assume that 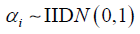 and
and 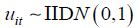 for all
i and t . For the values of γ , we let γ = 0.1, 0.5 and 0.8. We
consider the combination of sample size, T = 500, 1000 and T
= 10, 100, 200.
for all
i and t . For the values of γ , we let γ = 0.1, 0.5 and 0.8. We
consider the combination of sample size, T = 500, 1000 and T
= 10, 100, 200.
For the above DGP, we use the forward demeaning to eliminate the individual effects, αi , and we consider three estimators based on the forward differenced model, GMM based FOD using all lags as instruments (2.5), the double IV estimator (2.8) and the simple IV estimation using only one lag as instrument (Hsiao and Zhou, [9]). We calculate the mean (Mean), bias (Bias) as well as inter-quantile range (IQR) for the three estimators based on 2000 replications. The simulation results are summarized in Tables 1-3.
| T | N | 500 | 1000 | ||||
|---|---|---|---|---|---|---|---|
| GMM | Double IV | Simple IV | GMM | Double IV | Simple IV | ||
| 10 | Mean | 0.0975 | 0.1004 | 0.1007 | 0.0988 | 0.1005 | 0.0999 |
| Bias | -0.0025 | 0.0004 | 0.0007 | -0.0012 | 0.0005 | -0.0001 | |
| IQR | 0.0265 | 0.03 | 0.0322 | 0.0199 | 0.0214 | 0.0247 | |
| 100 | Mean | 0.0977 | 0.1001 | 0.0999 | 0.0988 | 0.1 | 0.0999 |
| Bias | -0.0023 | 0.0001 | -0.0001 | -0.0012 | 0 | -0.0001 | |
| IQR | 0.006 | 0.0064 | 0.0091 | 0.0045 | 0.0048 | 0.0065 | |
| 200 | Mean | 0.0977 | 0.1 | 0.0998 | 0.099 | 0.1001 | 0.1001 |
| Bias | -0.0023 | 0 | -0.0002 | -0.001 | 0.0001 | 0.0001 | |
| IQR | 0.0044 | 0.0049 | 0.0062 | 0.0031 | 0.0033 | 0.0043 |
Note: 1a) ?GMM? refers to the GMM estimator using all lags as IVs, ?Double IV? refers to the double filter IV estimator, and ?Simple IV? refers to simple IV estimator using only one lag variable as instrument.
1b) ?iqr? refers inter quantile range (25%-75%).
Table 1: Estimation results for different estimators of γ (γ = 0:1).
| T | N | 500 | 1000 | ||||
|---|---|---|---|---|---|---|---|
| GMM | Double IV | Simple IV | GMM | Double IV | Simple IV | ||
| 10 | Mean | 0.4936 | 0.5008 | 0.5003 | 0.4967 | 0.5006 | 0.4995 |
| Bias | -0.0064 | 0.0008 | 0.0003 | -0.0033 | 0.0006 | -0.0005 | |
| IQR | 0.0335 | 0.0421 | 0.0475 | 0.0246 | 0.0296 | 0.0357 | |
| 100 | Mean | 0.4966 | 0.5 | 0.4997 | 0.4983 | 0.5 | 0.4999 |
| Bias | -0.0034 | 0 | -0.0003 | -0.0017 | 0 | -0.0001 | |
| IQR | 0.0057 | 0.0063 | 0.0107 | 0.0043 | 0.0045 | 0.0078 | |
| 200 | Mean | 0.4968 | 0.5 | 0.4997 | 0.4985 | 0.5 | 0.5 |
| Bias | -0.0032 | 0 | -0.0003 | -0.0015 | 0 | 0 | |
| IQR | 0.0041 | 0.0044 | 0.0077 | 0.0028 | 0.003 | 0.0054 | |
Table 2: Estimation results for different estimators of  γ (γ = 0:5).
| T | N | 500 | 1000 | ||||
|---|---|---|---|---|---|---|---|
| GMM | Double IV | Simple IV | GMM | Double IV | Simple IV | ||
| 10 | Mean | 0.7745 | 0.8015 | 0.7992 | 0.7866 | 0.8011 | 0.7981 |
| Bias | -0.0255 | 0.0015 | -0.0008 | -0.0134 | 0.0011 | -0.0019 | |
| IQR | 0.051 | 0.0763 | 0.0889 | 0.0389 | 0.0548 | 0.0675 | |
| 100 | Mean | 0.7949 | 0.8 | 0.7994 | 0.7974 | 0.8 | 0.7997 |
| Bias | -0.0051 | 0 | -0.0006 | -0.0026 | 0 | -0.0003 | |
| IQR | 0.0047 | 0.0054 | 0.0132 | 0.0035 | 0.0039 | 0.0094 | |
| 200 | Mean | 0.7957 | 0.8 | 0.7996 | 0.7978 | 0.8 | 0.7999 |
| Bias | -0.0043 | 0 | -0.0004 | -0.0022 | 0 | -0.0001 | |
| IQR | 0.0032 | 0.0034 | 0.0089 | 0.0021 | 0.0023 | 0.0062 |
Table 3: Estimation results for different estimators of  γ (γ = 0:8).
From Tables 1-3, several interesting findings can be observed. On the one hand, we can observe that the GMM estimator for the forward differenced model using all lags behaves very similarly to the DIV estimator in terms of iqr, which is evident that these two estimators have similar asymptotic variance. When T is fixed, we can note that GMM using all available lags has the smallest IQR, which states that the GMM using all lags is more efficient than the DIV estimator for fixed T case. However, it is also clear that DIV is asymptotic unbiased since the bias of the estimates are almost negligible, while comparably there is significant bias for the GMM estimators using all lags as instruments. On the other hand, if only one lag is used in the estimation, the simple IV estimator is not as efficient as the GMM and DIV estimator in terms of IQR. In all, the findings in the simulation confirm our theoretical findings in the paper and DIV would be preferable choice for estimating dynamic panels in terms of unbiasedness and asymptotic efficiency.
Conclusion
In this paper, we establish the equivalence of the GMM estimator based on the forward differenced model using all lagged variables as instruments and the DIV estimator, which uses the deviate from the past mean lags as instruments. We provide mathematical equivalence for these two estimators for linear dynamic panel models. Monte Carlo simulations confirm the theoretical findings in this paper. We conclude that DIV would be preferable choice for estimating dynamic panels in terms of unbiasedness and asymptotic efficiency.
Acknowledgement
The author gratefully acknowledges the financial support from the National Natural Science Foundation of China (Grant No.71401166).
References
- Alvarez J, Arellano M. The time series and cross-section asymptotics of dynamic panel data estimators. Econometrica. 2003; 71: 1121-59.
- Anderson TW, Hsiao C. Estimation of dynamic models with error components. J Am Stat Assoc.1981; 76: 598-606.
- Anderson, TW, Hsiao C. Formulation and estimation of dynamic models using panel data, J Econom. 1982; 18: 47-82.
- Arellano M, Bond S. Some tests of specification for panel data: monte carlo evidence and an application to employment equations, Review of Economic Studies. 1991: 58: 277-97.
- Arellano M, Bover O. Another look at the instrumental variable estimation of error-components models, J Econom. 1995; 68: 29-51.
- Blundell R, Bond S, Windmeijer F. Estimation in dynamic panel data models: improving on the performance of the standard GMM estimator, in Nonstationary Panels, Panel Cointegration and Dynamic Panels, published online. 2000; 53-91.
- Hayakawa K. A simple efficient instrumental variable estimator for panel AR(p) models when both N and T are large, Econometric Theory. 2009; 25: 873-90.
- Hayakawa K, Qi M, Breitung B. Double filter instrumental variable estimation of panel data models with weakly exogenous variables, Working Paper, Hiroshima University. 2017.
- Hsiao C. Analysis of Panel Data 3rd edition, Cambridge University Press. 2014.
- Hsiao C, Zhou Q. First difference or forward demeaning: implications for the method of moments estimators, Econometric Reviews. 2017; 36: 883-97.