Research Article - Journal of Cardiovascular Medicine and Therapeutics (2017) Volume 1, Issue 2
Shock patients heart rate variability factors
Rabindra Nath Das*
Department of Statistics, The University of Burdwan, Kolkata, West Bengal, India
- Corresponding Author:
- Rabindra Nath Das
Department of Statistics
The University of Burdwan
Kolkata, West Bengal
India
Tel: +91-342-2558554
E-mail: rabin.bwn@gmail.com
Accepted Date: August 22, 2017
Citation: Das RN. Shock patients heart rate variability factors. J Cardiovasc Med Ther. 2017;1(2):19-23.
Abstract
Objectives: The current article identifies the shock patients heart rate variability factors. Specially, it aims to determine the mean and variance heart rate variability factors for shock patients.
Background: The casual factors of heart rate variability for shock patients are partially known in the literature. Methods: The response heart rate for shock patients is positive & heterogeneous. It may belong to exponential family distribution. Generally, joint generalized linear models (JGLMs) (Lognormal or gamma) fitting may be used.
Results: The mean hear rate decreases as the systolic blood pressure (BP) (SBP) (P=0.0281), or age (P<0.0001), or diastolic BP (DBP) (P<0.0001), or cardiac index (P<0.0001), or hematocrit (HCT) (P=0.0606), or mean circulation time (MCT) (P=0.0606) decreases, and vice versa. The mean heart rate is partially higher of female (P=0.1478) than male shock patients, and it is directly partially related with the shock types (P=0.1065). The heart rate response decreases as the mean arterial BP (MAP) (P<0.0001), or appearance time (AT) (P<0.0001), or body surface index (BSI) (P=0.1361) increases. It is inversely partially correlated with the card sequence (RECORD) (P= 0.0591). The heart rate variance decreases as the MAP (P=0.0110), or age (P=0.0055) increases. The heart rate variance is lower for female (P=0.0057), than male shock patients, and it is negatively partially associated with the shock types (P=0.1104). The heart rate variance increases as the diastolic BP (P=0.0615), or mean central venous pressure (MCVP) (P=0.0060), or urinary output (UO) (P=0.0076), or red cell index (RCI) (P=0.0243) increases.
Conclusion: Impacts of many factors such as gender, age, SBP, DBP, MAP, MCVP, CI, MCT, HCT, BSI, AT, RECORD on heart rate for shock patients have been derived based on statistical modeling. Many of the current results are new in the shock patients heart rate literature.
Keywords
Blood pressure, Cardiac index, Gamma models, Heart rate, Hematocrit, Red cell index.
Introduction
The heart rate is defined as the number of heart beats per minute (HBPM). Locating the heart rate changes casual factors of an individual by an expert cardiologist is really a difficult problem. Generally, heart rate depends on the body’s oxygen demand. Practically, many factors are responsible for a heart rate to vary inexplicably, or speed up, or slow down [1-5]. Medical doctors and practitioners use the measurement of heart beats per minute to select the appropriate medicine for proper treatment, or help in the diagnosis, or prescribe the exercise intensity, or tracking of medical conditions [6-9]. Recently, determinants of mean heart rate of some patients who underwent dobutamine stress echocardiography are derived in [9]. Some research articles based on cross-sectional and longitudinal studies have shown that aerobic endurance training accelerates heart rate recovery after exercise in healthy subjects [10-13].
Previous research articles [12,13] have used regression and meta-analysis to locate the heart rate determinants assuming the heart rate variance is constant. But the heart rate for shock patients in Statistical analysis [14] is a positive and non-constant variance response variable. Therefore, the heart rate data should be analysed based on joint gamma and Log-normal models [15- 21]. Best of our knowledge, there are some partial studies of heart rate for shock patients [14], using joint generalized linear models (JGLMs). These points motivated us to locate the shock patients heart rate determinants [14].
The present report aims to justify the following queries. What are the shock patients heart rate determinants? How are the determinants correlated with the heart rate? How are the determinants effecting on the heart rate? This information is not well-known in the shock study literature. The current article focuses the above hypotheses.
Statistical Methods and Data
Methods
Many positive continuous responses such as heart rates have non-normal probability distributions, and they are generally analyzed using Log-normal and gamma distribution [15-17].
For the analysis of positive data i y ’s, Nelder and Lee [17] proposed the joint generalized linear models (JGLMs), when
E(y i)=μi and Var(y i)=σi2μi2
where σi2’s are the dispersion parameters and V (μi2) is the variance function. In GLMs, the variance has two parts. One is V(μi) which dependents on the mean value changes, and the other is σi2, independent of mean adjustment. The variance function characterizes the GLM family distribution. For example, the distribution is Poisson if V(μ)=μ, normal if V(μ)= 1, gamma if V(μ)=μ2 etc.
JGLMs for the mean and dispersion parameters (proposed by Nelder and Lee [17]) are
η = g μi = χti β and εi = h σi2 = wtiγ
where g( μi) and h (σi2 ) are GLM link functions for the mean and the dispersion respectively; and xti, wti are respectively, the row vectors for the mean and the variance regression models. To estimate the mean model parameters, maximum likelihood (ML) method is used, and to estimate the dispersion model parameters, restricted ML (REML) method is used [16].
Shock data
The current shock data set is displayed in [14], and it is available at the sites: http://www.umass.edu/statdata/statdata/ data/shock.txt, or https://www.statcrunch.com/app/index.php? dataid=1327401.The shock data set includes 20 variables/ factors on 113 subjects. The data set has been collected at the Shock Research Unit, The University of Southern California, Los Angeles, California. The data set has two measurements on the same 113 ill patients and factors/variables. One is at the time of admission, and the other is at the time of discharge, or just before death. The patient population, shock types, data collection method is displayed in [14].
The 20 variables are age, sex (male=0, female=1), systolic BP (SBP), diastolic BP (DBP), type of shock (non-shock=1, hypovolemic=2, and bacterial, or cardiogenic, or neurogenic, or other=3), survival stage (survived=1, death=2), height, mean central venous pressure (MCVP), body surface index (BSI), mean arterial BP (MAP), cardiac index (CI), heart rate (HR), urinary output (UO), mean circulation time (MCT), appearance time (AT), hemoglobin (HG), plasma volume index (PVI), hematocrit (HCT), red cell index (RCI), card sequence (initial=1, final =2) (RCORD).
Analysis, Findings and Interpretations of Heart Rate of Shock Data
Analysis of heart rate
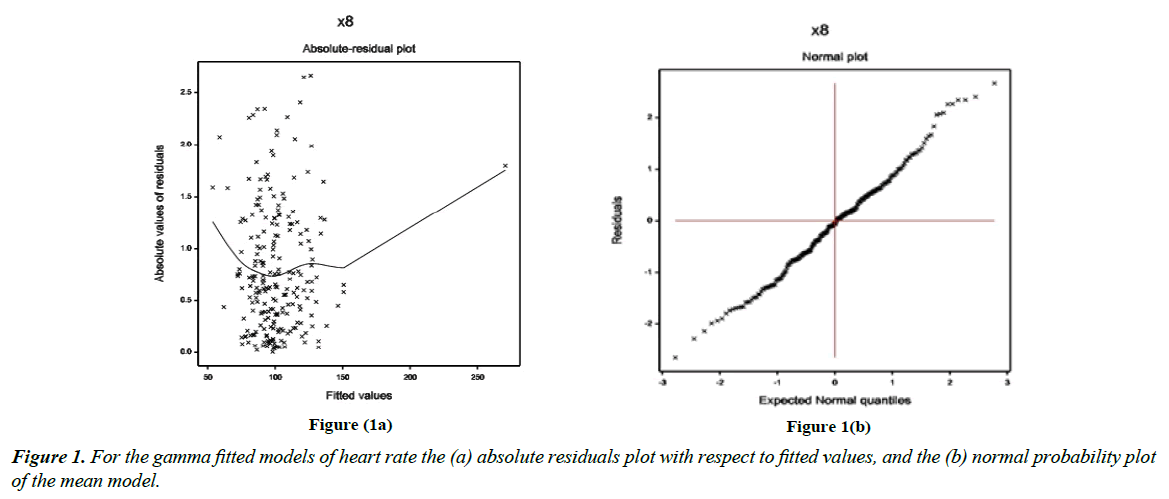
The heart rate for the shock patients is considered as the dependent variable, and the remaining others are treated as the independent variables. The JGLM Log-normal and gamma model analyses have been performed on the dependent variable heart rate based on the remaining other explanatory variables. Both the models give same results, so we have presented here the gamma models analysis results in Table 1. The analysis outcomes (or results) for both the mean and variance models are displayed in Table 1. Based on the lowest Akaike information criterion (AIC) value in each class, the final models have been selected. It is known that AIC selects a model which minimizes the predicted additive errors and the squared error loss (20, p. 203-204). Based on minimum AIC value (2023.387), the final fitted gamma models have been included in Table 1. The final considered models (Table 1) include some partially significant determinants (gender, shock types, BSI, MCT, DBP), which are considered as confounders in epidemiology. It is well-known that all the selected effects are not necessarily significant [20,21]. The JGLMs graphical analysis or diagnostic plots (residual and normal probability) of gamma fitted models (Table 1) have been presented in Figure 1.
Figure 1(a) reveals the absolute residual values plot with respect to fitted values. The residuals plot is exactly fat diagram with respect to running means except the right tail. The right tail is increasing due to a larger boundary value. Figure 1(b) presents the normal probability plot of the fitted gamma mean model (Table 1), which does not show any lack of fit.
| Model | Covariate | Estimate | Standard error | t-value | P-value |
|---|---|---|---|---|---|
| Mean Model | Constant | 4.0706 | 0.1817 | 22.39 | <0.0001 |
| Age (X1) | 0.0037 | 0.0010 | 3.46 | <0.0001 | |
| Sex (Fx 32) | 0.0490 | 0.0331 | 1.47 | 0.1408 | |
| Shock type (Fx 52) | 0.0551 | 0.0388 | 1.41 | 0.1579 | |
| Shock type Fx 53) | 0.0586 | 0.0361 | 1.62 | 0.1065 | |
| SBP (X6) | 0.0032 | 0.0014 | 2.21 | 0.0281 | |
| MAP (X7) | -0.0244 | 0.0044 | -5.47 | <0.0001 | |
| DBP (X9) | 0.0244 | 0.0041 | 6.78 | <0.0001 | |
| BSI (X11) | -0.1161 | 0.0775 | -1.49 | 0.1361 | |
| CI (X12) | 0.0848 | 0.0150 | 5.64 | <0.0001 | |
| AT (X13) | -0.0256 | 0.0065 | -3.87 | <0.0001 | |
| MCT (X14) | 0.0068 | 0.0035 | 1.88 | 0.0606 | |
| HCT (X19) | 0.0057 | 0.0024 | 2.37 | 0.0185 | |
| RECORD (Fx202) | -0.0563 | 0.0296 | -1.89 | 0.0591 | |
| Dispersion Model |
Constant | -2.4146 | 0.7782 | -3.103 | 0.0022 |
| Age (X1) | -0.0209 | 0.0075 | -2.803 | 0.0055 | |
| Sex (Fx 32) | -0.6112 | 0.2186 | -2.795 | 0.0057 | |
| Shock type (Fx 52) | -0.3872 | 0.3384 | -1.144 | 0.2539 | |
| Shock type (Fx 53) | -0.4852 | 0.3027 | -1.603 | 0.1104 | |
| MAP (X7) | -0.0411 | 0.0160 | -2.565 | 0.0110 | |
| DBP (X9) | 0.0367 | 0.0195 | 1.880 | 0.0615 | |
| MCVP (X10) | 0.0659 | 0.0238 | 2.773 | 0.0060 | |
| MCT (X14) | 0.0193 | 0.0132 | 1.464 | 0.1447 | |
| UO (X15) | 0.0024 | 0.0009 | 2.694 | 0.0076 | |
| RCI (X17) | 0.0453 | 0.0200 | 2.268 | 0.0243 |
Table 1: Results for mean and dispersion models of Gamma model fit of heart rate.
Results of heart rate
Table 1 shows the analysis of heart rate outputs for shock patients. From Table 1, it is observed that the mean heart rate is separately directly correlated with age (P< 0.0001), systolic BP (SBP) (P=0.0281), diastolic BP (DBP) (P< 0.0001), cardiac index (P< 0.0001), mean circulation time (MCT) (P=0.0606), hematocrit (HCT) (P=0.0606). The mean heart rate is separately inversely correlated with mean arterial BP (MAP) (P< 0.0001), body surface index (BSI) (P=0.1361), appearance time (AT) (P< 0.0001). The mean heart rate is negatively partially associated with the card sequence (RECORD) (P= 0.0591).
The heart rate variance is inversely correlated with the age (P=0.0055) and MAP (P=0.0110). The heart rate variance is lower for female (P=0.0057), than male shock patients, and it is negatively partially associated with the shock types (P=0.1104). The heart rate variance separately directly correlated with the DBP (P=0.0615), mean central venous pressure (MCVP) (P=0.0060), urinary output (UO) (P=0.0076), red cell index (RCI) (P=0.0243).
Interpretations of heart rate (HR) determinants
Mean model (Table 1) interprets the following:
1. The mean heart rate (MHR) for shock patients is positively associated with age (P< 0.0001), implying that the MHR decreases at the younger ages, and it increases at higher ages.
2. The MHR has partially positive correlation with the sex (female=1, male=0) (P=0.1408), implying that the MHR is lower for male shock patients than female.
3. The MHR is positively partially associated with the shock type (neurogenic, or bacterial, or cardiogenic, or other=3, hypovolemic=2, and non-shock=1) at level (hypovolemic=2) (P= 0.1579) and at level (neurogenic, or bacterial, or cardiogenic, or other=3) (P=0.1065), implying that the MHR is lower for the non-shock patients than shock patients with levels at 2 or 3.
4. The MHR is positively correlated with systolic BP (P=0.0281) for the shock patients, implying that the MHR decreases as systolic BP decreases, and vice versa.
5. The MHR is reciprocally correlated with the mean arterial BP (MAP) (P< 0.0001), indicating that MHR decreases as MAP increases.
6. The MHR is positively related with the diastolic BP (DBP) (P< 0.0001) for the shock patients, implying that MHR decreases as DBP decreases.
7. The MHR is negatively partially related with the body surface index (BSI) (P=0.1361), indicating that HR decreases as BSI increases.
8. The MHR is positively correlated with the cardiac index (CI) (P< 0.0001) for the shock patients, implying that the MHR decreases as CI decreases, and vice versa.
9. The MHR is inversely correlated with the appearance time (AT) (P< 0.0001), indicating that MHR decreases as AT increases.
10. The MHR is positively associated with mean circulation time (MCT) (P=0.0606), indicating that MHR decreases as MCT decreases, and vice versa.
11. The MHR is positively associated with mean hematocrit (HCT) (P=0.0185), indicating that HR decreases as HCT decreases, and vice versa.
12. The MHR is inversely related with card sequence (final=2, initial=1) (RCORD) (P=0.0591), implying that MHR is lower at the final stage.
13. Variance model (Table 1) interprets the following:
14. The heart rate variance (HRV) is negatively associated with the age (P=0.0055), implying that HRV decreases at the higher ages.
15. The HRV is reciprocally correlated with the gender, indicating that HRV is lower for female (P=0.0057), than male shock patients,
16. The HRV is inversely partially related with the shock types (P=0.1104), indicating that HRV is more for the non-shock patients than the other shocked patients.
17. The HRV is reciprocally correlated with the MAP (P=0.0110), indicating that HRV decreases as MAP increases.
18. The HRV is directly related with the diastolic BP (P=0.0615), implying that HRV decreases as DBP decreases.
19. The HRV is directly correlated with the mean central venous pressure (MCVP) (P=0.0060), implying that HRV decreases as MCVP decreases, and vice versa.
20. The HRV is directly related with the urinary output (UO) (P=0.0076), implying that HRV decreases as UO decreases, and vice versa.
21. The HRV is positively associated with the red cell index (RCI) (P=0.0243), implying that HRV decreases as RCI decreases, and vice versa.
22. The HRV is directly partially related with the mean circulation time (MCT) (P=0.1447), indicating that HRV decreases as MCT decreases, and vice versa.
Concluding Remarks
The heart rate variability factors for the shock patients are derived in Table 1. Effects of the determinants on heart rate have been described in the interpretation section. Here it is shown that both SBP & DBP are positively associated, while mean arterial BP is inversely correlated with mean heart rate. Mean circulation time, haematocrit, cardiac index, shock type and sex are also directly related with the mean heart rate. Body surface index, appearance time, and card sequence are reciprocally related with mean heart rate. Many determinants are related with the variance of heart rate. For example, age, sex, shock types, MAP are inversely correlated, while DBP, MCVP, MCT, UO, and RCI are directly related with the heart rate variance.
The current short research report has derived many casual factors of heart rate for shock patients. It is expected that the medical experts, general individuals, and shock patients will be benefited from the current findings. Heart rate may be considered along with the shock types, gender, age, blood pressure, cardiac index, urinary output etc. In addition, the present report shows many casual factors for the heart rate variability, and the current findings may be considered for better shock patients treatment.
Conflict of Interest
The author confirms that this article content has no conflict of interest.
Acknowledgement
The author is very much indebted to the referees who have provided valuable comments to improve the paper.
References
- Jose AD, Collison D. The normal range and determinants of the intrinsic heart rate in man. Cardiovasc Res. 1970;4:160-167.
- Graettinger WF, Smith DH, Neutel JM, et al. Relationship of left ventricular structure to maximal heart rate during exercise. Chest. 1995;107:341-345.
- American College of Sports Medicine. ACSM’s Guidelines for Exercise Testing and Prescription. 6th ed. Baltimore, MD: Lippincott Williams & Wilkins, 2000.
- Fletcher GF. How to implement physical activity in primary and secondary prevention: a statement for healthcare professionals from the Task Force on Risk Reduction, American Heart Association. Circulation. 1997;96:355-357.
- Boutcher SH, Stein P. Association between heart rate variability and training response in sedentary middle-aged men. Eur J ApplPhysiolOccup Physiol. 1995;70:75-80.
- Lauer MS. Autonomic function and prognosis. Cleve Clin J Med. 2009;76(Suppl 2):S18-S22.
- Sugawara J, Murakami H, Maeda S, et al. Change in post-exercise vagal reactivation with exercise training and detraining in young men. Eur J Appl Physiol. 2001;85:259-263.
- Javorka M, Zila I, Balharek T, et al. Heart rate recovery after exercise: relations to heart rate variability and complexity. Braz J Med Biol Res.2002;35:991-1000.
- Das RN. The mean heart rate associations of the DSE data. IntervCardiol J. 2017;3(1):1-3.
- Howley ET, Bassett DR, Welch HG. Criteria for maximal oxygen uptake: review and commentary. Med Sci Sports Exerc. 1995;27:1292-1301.
- Sugawara J, Murakami H, Maeda S,et al. Change in post-exercise vagal reactivation with exercise training and detraining in young men. Eur J Appl Physiol. 2001;85:259-263.
- Javorka M, Zila I, Balharek T, et al. Heart rate recovery after exercise: relations to heart rate variability and complexity. Braz J Med Biol Res.2002;35:991-1000.
- Gibbons RJ, Balady GJ, Beasley JW, et al. ACC/AHA guidelines for exercise testing: a report of the American College of Cardiology/ American Heart Association Task Force on Practice Guidelines (Committee on Exercise Testing). J Am CollCardiol. 1997;30:260-315.
- Afifi AA, Azen SP. Statistical analysis: A computer oriented approach, 2nd ed. Academic Press, New York, USA. 1979.
- Firth D. Multiplicative errors: Log-normal or gamma? J R Statist Soc B. 1988;50:266-268.
- Das RN, Lee Y. Log normal versus gamma models for analyzing data from quality-improvement experiments. Qual Engineering. 2009;21(1):79-87.
- Nelder JA, Lee Y. Generalized linear models for the analysis of Taguchi-type experiments. Applied Stochastic Models and Data Analysis. 1991;7:107-120.
- Das RN. Hypertension risk factors who underwent dobutamine stress echocardiography. Interv. Cardiol. 2016;8(1):595-605.
- Lee Y, Nelder JA, Pawitan Y. Generalized linear models with random effects (Unified analysis via H-likelihood). Chapman & Hall, London, 2006.
- Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. Springer-Verlag, NewYork, 2001.
- Das RN. Robust response surfaces, regression, and positive data analyses. Chapman & Hall, London, 2014