Research Article - Biomedical Research (2019) Volume 30, Issue 6
Numerical study of the influence of ultra-thin veneer materials and its thickness on their biomechanical behavior
Ayham Darwich1,2*, Mayssa Shash2, Ali Ali2, Hasan Nazha2, Ali Marouf3, William Abbas41Department of Biomedical Engineering, Al-Andalus University for Medical Sciences, Tartous, Syria
2Department of Technical Engineering, University of Tartous, Tartous, Syria
3Department of Dentistry, University of Tartous, Tartous, Syria
4Department of Mechanical Engineering, Czech Technical University, Prague, Czech Republic
- *Corresponding Author:
- Ayham Darwich
Department of Biomedical Engineering
Al-Andalus University for Medical Sciences
Tartous,Syria
Accepted Date: November 07, 2019
Abstract
This study investigated the influence of ultra-thin veneer materials and its thickness on their
biomechanical behavior using the 3D finite element method to find out which of all these models have a
better performance. The distribution of stresses in the models was studied when composite resin and
feldspathic porcelain were used in ultra-thin veneers with thickness of 0.2 mm and 0.3 mm under static
loads. The results showed that the use of composite resin in the preparation of veneer of 0.2 mm in
thickness reduces the maximum stresses by 65.24% at least compared to feldspathic porcelain, and it
reduces the maximum stresses by 56.28% at least compared to feldspathic porcelain in veneer with
thickness of 0.3 mm. The results showed also that the use of composite resin ultra-thin veneer with
thickness of 0.2 mm reduces the maximum stresses by 49.48% at least compared to veneer with
thickness of 0.3 mm, and the using of feldspathic porcelain ultra-thin veneer with thickness of 0.2 mm
reduces the maximum stresses by 36.46% at least compared to veneer with thickness of 0.3 mm.
Therefore, it is recommended to use composite resin ultra-thin veneer with thickness of 0.2 mm as it
reduces induced stresses, which improves the stability and durability of veneers and prolong its lifespan.
Keywords
Ultra-thin veneers, Preparation materials, Veneer thickness, Biomechanical behavior, Finite element analysis.
Introduction
The development of dental restorations is constantly increasing, which is associated with an increasing interest for obtaining beautifully restored teeth using cosmetic veneers to restore and beautify faded, deformed or worn teeth, especially those that located in the visible areas of the mouth [1]. Biocompatible porcelain and composite resins are the most widely applied materials used in dentistry as restoration and veneer materials, regards it has characteristics similar to those of the dentin [2], and has a similar flexible module and strength when it used for direct or indirect restorations [3]. As for ceramic materials, it has a modulus of elasticity similar to that of the enamel layer [4,5].
The wrong choice of cosmetic veneer material and its thickness is one of the most important factors leading to failure. In the reports of success rates of veneer designs, there was a success rate ranging from 72%-85% for two veneer designs (palatal chamfer and butt-joint designs) in a five-year survey [6]. The most failure cases may be attributed to the veneer fracture and the adhesion weakness on the tooth surface [7]. As reported, the incisor and cervical region were the most likely to fail [8,9]. Thus, the veneer designs are the most important factors affecting long-term clinical success. In order to determine the success or failure rate of veneers, the stress distribution analysis should be performed using the 3D finite element method, which is the most efficient and effective tool in such cases [10-12]. The importance of this research is mainly to maintain as much tooth structure as possible by using ultra-thin cosmetic veneers, and to overcome the majority of failure cases that may occur as a result of the wrong selection of ultra-thin veneer design by studying the stress distribution in cosmetic veneers using two different materials (composite resin and feldspathic porcelain) and different preparation thicknesses (0.2 mm and 0.3 mm) for these veneers, which is affecting the biochemical behavior of teeth restored with veneers. Therefore, the aim of this research is to find out the veneer material and thickness that have the best performance to be used in the preparation of dental veneers.
Materials and Methods
Modeling and Meshing
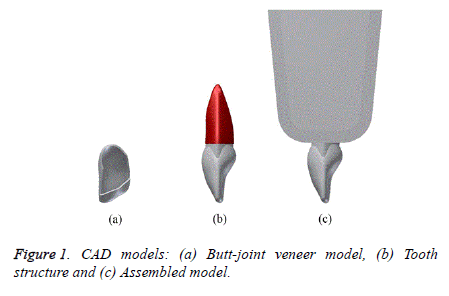
3D models were established using Autodesk® InventorTM software for incisor tooth structure, including the enamel with a thickness of 0.3 mm and the dentin. The tooth root was also surrounded by the periodontal ligament with a thickness of 0.2 mm. A section of the upper jawbone was then established, including cancellous bone surrounded by cortical bone with a thickness of 2 mm. Then the butt-joint models with a thickness of 0.2 mm and a thickness of 0.3 mm were created for the various cosmetic veneers to be studied as shown in Figure 1. All these models were then exported to the ANSYSTM software to perform the finite element analysis (FEA).
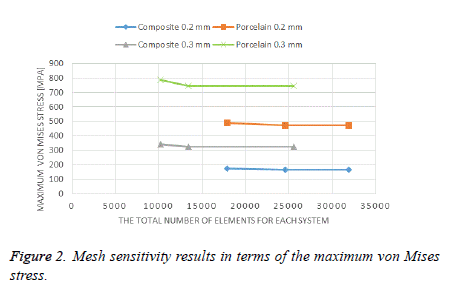
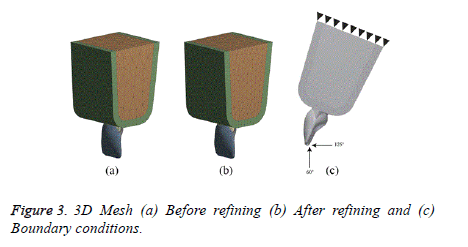
Due to the complexity of the geometry of the studied models, the mesh with tetrahedral elements was used. The mesh was refined and accepted when the relative errors were less than 1% [13]. The results of convergence analysis are shown in Table 1 and Figure 2. The mesh of studied models before and after refinement is shown in Figure 3.
| Components | 0.2 mm thick | 0.3 mm thick | ||
|---|---|---|---|---|
| Elements | Nodes | Elements | Nodes | |
| Periodontal ligament | 962 | 1970 | 962 | 1970 |
| Dentin | 2669 | 4521 | 2747 | 4644 |
| Enamel | 12530 | 21426 | 573 | 1291 |
| Veneer | 863 | 1822 | 1284 | 2597 |
| Cortical bone | 3489 | 6528 | 3489 | 6528 |
| Cancellous bone | 4357 | 4357 | ||
Table 1: Total number of elements and nodes for each component.
Boundary conditions
A load of 10 N with the 125° (protrusion) and 60° (tearing) angles with the tooth’s longitudinal axis were applied at the palatal surface of the veneer as shown in Figure 3 [14]. All contact conditions established in this FE analysis are considered bonded [15-21]. The FEM model is fixed at the top surface of the maxilla as shown in Figure 3.
Material properties
All materials of the studied components were considered to be linear elastic isotropic, taking into consideration that isotropic materials show the same mechanical properties regardless of loading direction [22]. The reference values are taken from previous studies [23-27]. Table 2 shows a summary of the mechanical properties used in this study.
| Material | Elastic modulus E [GPa] | Poisson’s ratio ν |
|---|---|---|
| Periodontal ligament | 0.069 | 0.45 |
| Dentin | 18.6 | 0.31 |
| Enamel | 80 | 0.33 |
| Composite resin | 14.74 | 0.33 |
| Feldspathic porcelain | 70 | 0.19 |
| Cortical bone | 13.7 | 0.3 |
| Cancellous bone | 1.37 | 0.3 |
Table 2: Mechanical properties of the materials used in the study.
Results and Discussion
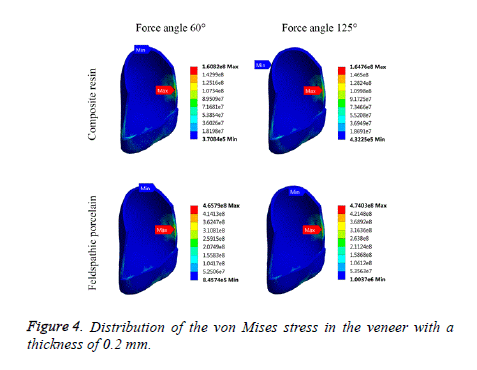
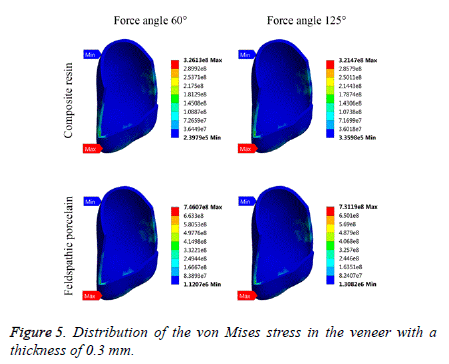
The data obtained from the finite element analysis can be presented in a stress distribution map with a color scale, which makes it possible to directly compare the magnitude and distribution of stress of various models. These results demonstrate the relationship between the stress distribution in the veneer-tooth structure system and the materials of the veneer models (Figures 4 and 5). One of the theories most used to determine the stress is von Mises theory [28]. This theory has been applied to determine the stress distribution of the models. From the FE analysis, the numerical results of maximum von Mises stress obtained from different models have been tabulated in Table 3.
| Von Mises Stress [MPa] | ||||
|---|---|---|---|---|
| Component | 0.2 mm thick | 0.3 mm thick | ||
| 125° | 60° | 125° | 60° | |
| Composite resin | 164.76 | 160.82 | 321.47 | 326.13 |
| Feldspathic porcelain | 474.03 | 465.79 | 731.19 | 746.07 |
Table 3: Maximum von Mises stress according to the veneer material and thickness.
It could be noted from Figures 4 and 5 that the stress distribution does not differ according to the applied forces or the material used, but the stress distribution varies according to the thickness of the cosmetic veneer. Maximum stresses are concentrated in the lateral edge of the veneer with a thickness of 0.2 mm. For veneer with a thickness of 0.3 mm, maximum stress is concentrated around the incisal area.
Returning to the results presented in Table 3, it is noted that the use of composite resin material for the preparation of cosmetic veneer with a thickness of 0.2 mm reduces the maximum stress by at least 65.24% compared with feldspathic porcelain material, while its use of the preparation of veneer with a thickness of 0.3 mm reduces the maximum stress by at least 56.28% compared with feldspathic porcelain material.
These results can be explained by the fact that the use of composite resin material can distribute the applied loads more homogeneous than the other material, which is affecting the reduction of stress concentration in the veneer-tooth structure system. Therefore, the use of this material for the preparation of ultra-thin veneer could improve the stability and durability of the system and prolong its lifespan.
From Table 3, it is noted also that the use of the composite resin veneer with a thickness of 0.2 mm reduces the maximum stress by at least 49.48% compared with the veneer with a thickness of 0.3 mm, while its use of the preparation of feldspathic porcelain veneers reduces the maximum stress by at least 36.46% compared with the veneer with a thickness of 0.3 mm.
These results can be explained by the fact that the use of ultrathin veneer with a thickness of 0.2 mm maintains the thickness of 0.1 mm of the tooth enamel, which leads to a greater reduction of the induced stress compared to the use of the veneer with a thickness of 0.3 mm that lead to remove the entire enamel and adhere to the dentin, that could increase the values of the induced stress in dental veneer.
Although there is no similar study of the influence of ultra-thin veneer materials and its thickness on their biomechanical behavior, but there are many studies have indicated that the stresses concentrated in the incisal area [14,29], which was in agreement with the presented results in this study. Li et al. studied the effect of veneer materials with the thickness of 0.5 mm on its biomechanical behavior using the finite element analysis [25]. They found that the use of the composite resin model showed a more homogeneous behavior than porcelain model. This result was in agreement with the presented results in this study. Ge et al. found in their in vitro study that the porcelain veneer adhered to the enamel performs better than the one that adhered to the dentin, and this result is fully consistent with the results of this study [30]. Their results showing a good agreement with the results in this study.
Conclusion
The use of composite resin material in the preparation of ultrathin veneer reduces the maximum stress induced in the model, whatever the thickness used in its preparation. The use of ultrathin veneer with a thickness of 0.2 mm reduces the maximum stress induced in the model, whatever the material used in its preparation. Based on these results, it is not recommended to use feldspathic porcelain in the preparation of ultra-thin veneer, but it is recommended to use the composite resin. It is also not recommended to use the veneer with a thickness of 0.3 mm, but it is recommended to use ultra-thin veneer with a thickness of 0.2 mm, which improves the stability and durability of the cosmetic restoration and prolong its lifespan.
References
- Belser UC, Macne P, Macne M. Ceramic laminate veneers: Continuous evolution of indications. J Esthet Restor Dent 1997; 9: 197-207.
- Dejak B, Mlotkowski A. Three-dimensional finite element analysis of strength and adhesion of composite resin versus ceramic inlays in molars. J Prosthet Dent 2008; 99: 131-140.
- Cesar PF, Júnior WGM, Braga RR. Influence of shade and storage time on the flexural strength, flexural modulus, and hardness of composites used for indirect restorations. J Prosthet Dent 2001; 86: 289-296.
- Habelitz S, Marshall SJ, Marshall Jr GW, Balooch M. Mechanical properties of human dental enamel on the nanometre scale. Archives of Oral Biology 2001; 46: 173-183.
- Albakry M, Guazzato M, Swain MV. Biaxial flexural strength, elastic. J Prosthet Dent 2003; 89: 374-380.
- Guess PC, Stappert CF. Midterm results of a 5-year prospective clinical investigation of extended ceramic veneers. Dent Mat 2008; 24: 804-813.
- Peumans M, Van Meerbeek B, Lambrechts P, Vanherle G. Porcelain veneers: A review of the literature. J Dent 2000; 28: 163-177.
- Castelnuovo J, Tjan AH, Phillips K, Nicholls JI, Kois JC. Fracture load and mode of failure of ceramic veneers with different preparations. J Prosthet Dent 2000; 83: 171-180.
- Stappert CFJ, Stathopoulou N, Gerds T, Strub JR. Survival rate and fracture strength of maxillary incisors, restored with different kinds of full veneers. J Oral Rehabil 2005; 32: 266-272.
- Ausiello P, Apicella A, Davidson CL, Rengo S. 3D-finite element analyses of cusp movements in a human upper premolar, restored with adhesive resin-based composites. J Biomech 2001; 34: 1269-1277.
- Matson MR, Lewgoy HR, Barros Filho DA, Amore R, Anido-Anido A. Finite element analysis of stress distribution in intact and porcelain veneer restored teeth. Comput Methods Biomech Biomed Eng 2012; 15: 795-800.
- Shash M, Nazha H, Abbas W. Influence of Different Abutment Designs on the Biomechanical Behavior of One-Piece Zirconia Dental Implants and Their Surrounding Bone: A 3D-FEA. IRBM 2019; 5.
- Darwich A, Nazha H, Daoud M. Effect of Coating Materials on the Fatigue Behavior of Hip Implants: A Three-dimensional Finite Element Analysis. Journal of Appl Computat Mech 2019.
- Zarone F, Apicella D, Sorrentino R, Ferro V, Aversa R. Influence of tooth preparation design on the stress distribution in maxillary central incisors restored by means of alumina porcelain veneers: A 3D-finite element analysis. Dent Mater J 2005; 21: 1178-1188.
- Coelho PG, Bonfante EA, Silva NRF, Rekow ED, Thompson VP. Laboratory simulation of Y-TZP all-ceramic crown clinical failures. J Dent Res 2009; 88: 382-386.
- Marshall Jr GW, Balooch M, Gallagher RR, Gansky SA, Marshall SJ. Mechanical properties of the dentinoenamel junction: AFM studies of nanohardness, elastic modulus, and fracture. J Biomed Mater Res A 2001; 54: 87-95.
- Dejak B, Mlotkowski A. Three-dimensional finite element analysis of strength and adhesion of composite resin versus ceramic inlays in molars. J Prosthet Dent 2008; 99: 131-140.
- Lanza A, Aversa R, Rengo S, Apicella D, Apicella A. 3D FEA of cemented steel, glass and carbon posts in a maxillary incisor. Dent Mater J 2005; 21: 709-715.
- Yettram AL, Wright KWJ, Houston WJB. Centre of rotation of a maxillary central incisor under orthodontic loading. Br J Orthod 1977; 4: 23-27.
- Friedman CM, Sandrik JL, Heuer MA, Rapp GW. Composition and mechanical properties of gutta-percha endodontic points. J Den Res 1975; 54: 921-925.
- Okamoto K, Ino T, Iwase N, Shimizu E, Suzuki M. Three-dimensional finite element analysis of stress distribution in composite resin cores with fiber posts of varying diameters. Dent Mater J 2008; 27: 49-55.
- Darwich A, Nazha H, Abbas W. Numerical study of stress shielding evaluation of hip implant stems coated with composite (carbon/PEEK) and polymeric (PEEK) coating materials. Biomed Res 2019; 30: 169-174.
- Jones DW, Jones PA, Wilson HJ. The modulus of elasticity of dental ceramics. Dent Practition Dent Rec 1972; 22: 170-173.
- Rocha EP, Anchieta RB, Freitas-Junior AC, De Almeida EO. Mechanical behavior of ceramic veneer in zirconia-based restorations: a 3-dimensional finite element analysis using microcomputed tomography data. J Prosthet Dent 2011; 105: 14-20.
- Li Z, Yang Z, Zuo L, Meng Y. A three-dimensional finite element study on anterior laminate veneers with different incisal preparations. J Prosthet Dent 2014; 112: 325-333.
- Chuang SF, Chen TY, Chang CH. Application of digital image correlation method to study dental composite shrinkage. Strain 2008; 44: 231-238.
- Papadogiannis DY, Lakes RS, Papadogiannis Y, Palaghias G, Helvatjoglu-Antoniades M. The effect of temperature on the viscoelastic properties of nano-hybrid composites. Dent Mater J 2008; 24: 257-266.
- Beer FB, Johnston ER. Mechanics of materials. New York: McGraw-Hill. 1981; 616 pp.
- Sorrentino R, Apicella D, Riccio C, Gherlone E, Zarone F. Nonlinear visco‐elastic finite element analysis of different porcelain veneers configuration. J Biomed Mater Res B Appl Biomater 2009; 91: 727-736.
- Ge C, Green CC, Sederstrom DA, McLaren EA, Chalfant JA. Effect of tooth substrate and porcelain thickness on porcelain veneer failure loads in vitro. J Prosthet Dent 2018; 120: 85-91.