Research Article - Journal of Industrial and Environmental Chemistry (2017) Volume 1, Issue 1
Numerical investigation of separation of metals by non-steady-state cyclic counter-current liquid-liquid extraction
Vera V Belova*Institute of General and Inorganic Chemistry, Russian Academy of Sciences, Moscow, Russia
- *Corresponding Author:
- Vera V Belova
Institute of General and Inorganic Chemistry
Russian Academy of Sciences
Moscow
Russia
Tel: +7-495-955-4834
E-mail: belova@igic.ras.ru
Accepted Date: September 20, 2017
Citation: Belova VV. Numerical investigation of separation of metals by non-steady-state cyclic counter-current liquid-liquid extraction. J Ind Environ Chem. 2017;1(1):1-6
Abstract
Using the extraction of chlorides of Cu, Ni, Zn, Fe as the model system, we report our numerical studies on metal separation by the method of non-steady-state cyclic (dynamic) counter-current liquid-liquid extraction. The experimental data on distribution of chlorides of Cu, Ni, Zn, and Fe in the binary extractant system were used for simulation of separation processes of metals. Numerical studies on the dynamic counter-current extraction have shown that with increasing sample loading time the separation of metals decreases, whereas with increasing number of extraction stages fewer cycles are required for metal separation.
Keywords
Dynamic counter-current liquid-liquid extraction, Calculation program, Numerical researches, Metal separation, Metal chloride extraction
Introduction
There are two main directions of researches to improve the performance of solvent extraction methods for recovery, separation and purification of metals: 1) development and study of extraction systems; 2) application of highly efficient process schemes and modes of operation. Within the first direction we have examined the systems involving binary extractants for the extraction and separation of different metals [1-3]. Binary extractants (salts of organic acids with organic bases) can be considered as a particular case of ionic liquids. It has been found that binary extractant systems are characterized by reversibility of extraction and stripping processes [1]. For practical purposes, binary extractants involving strong organic acids (for example, dinonylnaphthalenesulphonic acid) are of the most interest, since stripping processes in these systems can be performed under much milder conditions.
Another trend in the development of new separation methods appears to be an application of the principle of solid support free liquid-liquid chromatography [4]. Unlike to the classical chromatography, the so-called stationary phase in the solid support free liquid-liquid chromatography is mobile, because it is not fixed on the stationary solid support and is retained in the chromatographic device in a free (mobile) state by centrifugal forces [4,5] or forces of viscosity and surface tension [6]. Intermittent dual (cyclic dual-mode) countercurrent chromatography (CCC) has been extensively studied [6-11]. The analysis of eluent column chromatography for cyclic and stationary modes of flow of mobile phase showed a higher degree of separation achieved in the cyclic mode [12]. In cyclic dual-mode processes, the CCC separation consists of a succession of two counter-current steps and is carried out in series alternating between the upper and the lower phase flow periods [7,8]. This combination of the processes of liquid chromatography and counter-current extraction allows developing novel high efficiency separation processes, which can be called dynamic counter-current extraction. Each cycle of such counter-current processes consists of two steps (halfperiods): 1 - a step of the flow of an initial solution (raffinate phase) and 2 - a step of the flow of an extractant (extract phase). Ito Y [4] and Kostanyan AE et al. [5] studied the cyclic mode process with variable duration of the periods of the phase flows. The sample dissolved in the raffinate phase is continuously fed into a CCC column at the beginning of the first step of the first cycle over a constant time, not exceeding the run time of the first step. In conducting such a cyclic process, the phase flow in the extraction-chromatographic unit is repeatedly switched back and forth at given intervals to retain the solutes inside the column as long as a separation of the components is reaching. Consequently, it is increasing the way of sample movement in the column, which increases the efficiency of the separation of components. During the movement of the sample in the column along with the separation of components an expansion of peaks is observed because of interfacial mass transfer and longitudinal mixing [13]. To hold the sample in the column for a predetermined number of cycles a decrease in the duration of the flow of the phases is needed from cycle to cycle. In Kostanyan AE et al. [11] equations were developed allowing the simulation of the chromatograms eluted from the column with the phases during each step of the cycles.
The objective of this study was to analyze the possibilities of using the dynamic counter-current extraction for the separation of metals, in particular non-ferrous metals, and iron. For this purpose, the extraction of metal chlorides from 2 M HCl solutions with the binary extractant such as methyltrioctylammonium dinonylnaphthalenesulphonate was investigated. The experimental data were used for calculation studies of metal salts separation by dynamic counter-current extraction.
Experimental
Chemicals and reagents
A solution of methyltrioctylammonium dinonylnaphthalenesulphonate (binary extractant) in toluene was employed for the extraction. Dinonylnaphthalenesulphonic acid was obtained from Sigma Aldrich and methyltrioctylammonium chloride was obtained from Acros Organics, and the extractants were used without further purification. Binary extractant was prepared by dissolving equimolar amounts of methyltrioctylammonium chloride and dinonylnaphthalenesulphonic acid in toluene, followed by shaking the organic solution with an equal volume of 1 M NaOH solution for 10 min and followed by washing the organic phase with water. Stock solutions of chlorides of nickel(II), copper(II), zinc(II), and iron(III) were prepared by dissolving of metal chlorides in 2 M HCl solution. All chemicals used were of analytical grade.
Solvent extraction procedure
The metal extraction with equal volumes of the aqueous and organic phases was carried out at 20°C. Samples in test tubes with ground-in stoppers were shaken mechanically. The duration of phase mixing was 15 min which was sufficient to establish the equilibrium values of the distribution coefficients of the metals.
Analysis
After separation of the layers, a suitable aliquot of the aqueous phase was analyzed by the complexometric titration method. Concentrations of nickel, copper, zinc, and iron in aqueous solutions were analyzed by titration with a standard solution of EDTA using murexide or eriochrome black T as the indicators [14]. The concentrations of metals in the organic phase were determined by the differences between the concentrations in the initial solutions and the aqueous phases after extraction. Experimental data on the extraction of metal chlorides from 2 M HCl solutions with solutions of methyltrioctylammonium dinonylnaphthalenesulphonate in toluene are given in Table 1.
Table 1. Experimental data on the extraction of metal chlorides from 2 M HCl with solutions of methyltrioctylammonium dinonylnaphthalenesulphonate in toluene.
| Concentration of extractant, M | Initial metal concentration | Distribution coefficients of metals, KD | |||
|---|---|---|---|---|---|
| M | Ni | Cu | Fe | Zn | |
| 0.05 | 0.025 | 0.2 | 0.57 | 1.27 | 0.11 |
Theoretical Studies on Separation of Metals
For theoretical studies on separation of metals by dynamic counter-current extraction, the calculating machine presented in the online version of the paper [11] was used.
Brief description of calculating machine
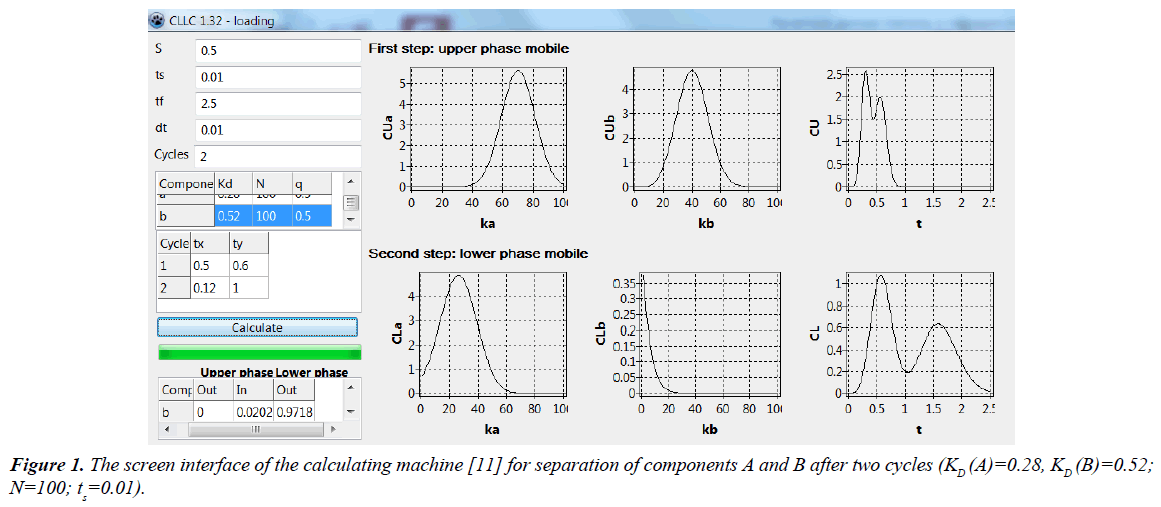
Figure 1 shows the interface of calculating machine with using the separation of two metals (A and B) as an example.
The input parameters are set in the windows provided above the button “calculate” of the display: S – the fractional volume of the lower phase (0.5); ts – dimensionless sample loading time (0.01); tf – dimensionless eluting time if both solutes would have completely eluted during each step of the current cycle (2.5); dt – calculation interval (0.01); Cycles – the current cycle number, for which the concentration profiles are presented (2); Component: for solutes A and B are given the values of KD (distribution coefficients) equal to 0.28 and 0.52 respectively, N – the number of theoretical plates (100 and 100; in general, can be different for each solute); q – the portions of each solute in the sample (0.5 and 0.5); Cycle - duration of phase elution steps in each cycle for all cycles from the first up to the current (1, 2): tx – upper phase mobile (in the first cycle – 0.5, in the second cycle – 0.12), ty – lower phase mobile (0.6 and 1 respectively). In the windows below the button “calculate”, the results of calculation of retained (In) and eluted (Out) portions of each solute for current cycle are given. On the right side of the display the calculated diagrams for the current cycle (2) are shown: the profiles of dimensionless concentrations of solutes A (a) and B (b) in the upper phase in the column at the end of each step (for the first step – CUa, CUb, and for the second step – CLa, CLb; ka and kb are the current cell numbers for each solute); the chromatograms for the case, when both solutes would have completely eluted during each step of the current cycle. For calculating the chromatograms, when both solutes are completely eluted during each step of the current cycle (CU and CL) the following expressions were used [11]:
CU = qaXaj(t) + qbXbj(t) (1)
CL = qaYaj(t) + qbYbj(t), (2)
Where, qa = Qa/(Qa + Qb); qb = Qb/(Qa + Qb). Values of Qa and Qb are the amounts of components in the sample; X(t) - solute concentration in the upper phase, Y(t) - solute concentration in the lower phase. It should be noted that the concentrations CU and CL in Eqs. (1) and (2) are normalized using the average concentration in the column: x̄ = Q/Vc = (Qa + Qb)/Vc (Vc - the column volume, Vc = VU + VL).
Results and Discussion
Numerical studies of metal separation
Using the experimental values of distribution coefficients of metal chlorides (Table 1) numerical studies and modelling of separation of metals by the method of dynamic counter-current extraction were carried out. In [11], the method of dynamic counter-current extraction is called as multiple dual-mode counter-current chromatography with variable duration of phase elution steps. Using the program it is possible to calculate the relative proportions of two components to be separated, which remain in the extraction system (for example, in a cascade of mixer-settlers), as well as the proportions of these components, which are removed out of the system with phase flow in each cycle of the process.
Separation of binary mixtures
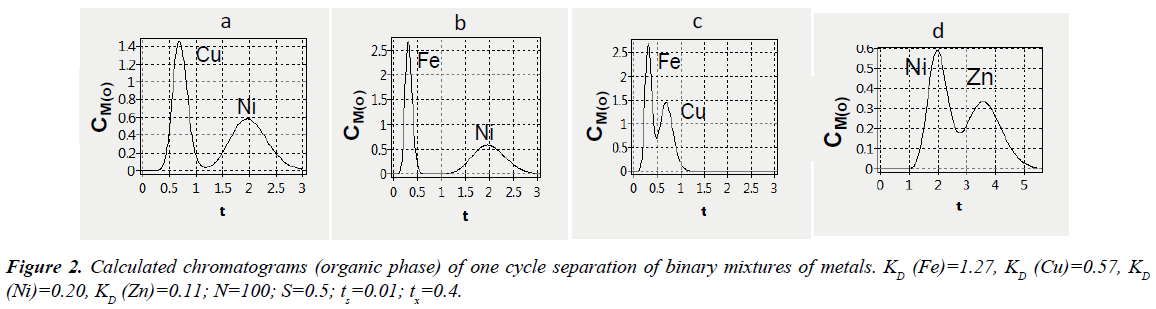
The numerical researches of separation of metal mixtures depending on various parameters were carried out. It was assumed that the process starts with feeding the first (aqueous) phase, which is a mixture of metal salts. The distribution coefficient (KD) is the ratio of metal concentration in the second (organic) phase to metal concentration in the first (aqueous) phase. In calculations, the following parameters were set: the number of theoretical plates (equilibrium extraction stages N), variable values of dimensionless time of phase movements (tx and ty) to achieve the best possible separation of metal mixtures. It should be noted that after feeding a metal mixture in the first half period of one cycle at first the metal with less distribution coefficients is coming out of an extraction system and in the second half period of cycle the reverse order of output of metals is observed. The calculated data for separation of binary mixtures of metals, which distribution coefficients differ significantly, indicated that individual metals are separated entirely within one cycle. As it follows from Figure 2, all the metals are eluting successively with the same (organic) phase in the second half period of the first cycle. Nickel and copper (a), iron and nickel (b) can be effectively separated within one cycle, whereas the separation of iron and copper (c), nickel and zinc (d) is complicated because their distribution coefficients are distinguished less.
Separation of three component mixtures
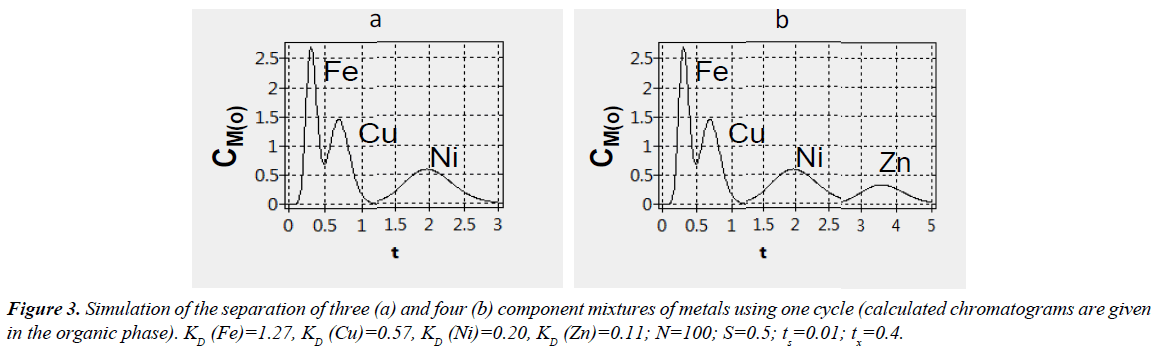
The above described program provides separation of binary mixtures [11] but the program can be used for calculating separation of three and more components. Initially using the program the data for the separation of different binary mixtures of metals were calculated (Figures 2a-2c). Then the total chromatograms were plotted on the basis of the results obtained. In Figure 3a and Table 2 the simulation of the separation of three metals (nickel, copper and iron) by using the program is shown.
Table 2. The calculation results of the separation of nickel, copper and iron for N=100 (KD: 0.57 (Cu), 0.20 (Ni), 1.27 (Fe); ts=0.01).
| tх | Relative proportions of metals in 1 half period (aqueous phase) | ||||||
|---|---|---|---|---|---|---|---|
| Ni | Cu | Fe | |||||
| In | Out | In | Out | In | Out | ||
| 0.4 | 0.9999 | 0.0001 | 1 | 0 | 1 | 0 | |
| 0.58 | 0.6521 | 0.3479 | 0.9983 | 0.0017 | 1 | 0 | |
| tх | tу | Relative proportions of metals in 2 half period (organic phase) | |||||
| Ni | Cu | Fe | |||||
| In | Out | In | Out | In | Out | ||
| 0.4 | 0. 5 | 0.9999 | 0 | 0.9419 | 0.0581 | 0.0142 | 0.9858 |
| 1.5 | 0.9366 | 0.0634 | 0.0002 | 0.9417 | 0 | 0.0142 | |
| 4 | 0 | 0.9356 | 0 | 0.0002 | |||
| 0.58 | 0.65 | 0.6521 | 0 | 0.9911 | 0.0073 | 0.025 | 0.975 |
| 1.7 | 0.6515 | 0.0006 | 0.0001 | 0.991 | 0 | 0.025 | |
| 4 | 0.0001 | 0.6514 | 0 | 0.0001 | |||
Table 2 summarizes the relative proportions of nickel, copper and iron after one cycle of counter-current extraction process for different values of the relative time durations of the first (tх) and second (ty) half-periods. In the first case (tх=0.4), three fractions of the organic phase containing iron, copper and nickel (Figure 3a) are obtained in the following sequence: Fe fraction (ty=0.5) in a yield of 98.6% and a purity of 94.4%, Cu fraction (ty=1.5) in a yield of 94.2% and a purity of 92.4%, Ni fraction (ty=4) in a yield of 93.5% and a purity of 100%. In the second case (tх=0.58), during the first half-period 34.8% of Ni flows out with the aqueous phase, and during the second half-period (organic phase) 97.5% of iron with a purity of 99.3% (ty=0.65), 99.1% of copper with a purity of 99.9% (ty=1.7) and 65.1% nickel with a purity of 100% (ty=4) flow out successively. The calculated results (Table 2) show that, when tх = 0.58, better separation of iron and copper is observed, however, in the first case (tх=0.4) all metals come out completely during second halfperiod of one cycle. It is evident that reducing the number of stages (e.g., column) operating expenses decrease, therefore, the calculated data for the separation of three metals at N equal to 50 were obtained (Table 3).
Table 3. The calculation results of the separation of nickel, copper and iron for N=50(KD: 0.57 (Cu), 0.20 (Ni), 1.27 (Fe); ts=0.01).
| Cycle | tх | tу | Relative proportions of metals in 1 half period (aqueous phase) | |||||
|---|---|---|---|---|---|---|---|---|
| Ni | Cu | Fe | ||||||
| In | Out | In | Out | In | Out | |||
| 1 | 0.43 | 0.15 | 0.9887 | 0.0113 | 1 | 0 | 1 | 0 |
| 2 | 0.2 | 0.5 | 0.5041 | 0.4845 | 0.9862 | 0.0138 | 0.9839 | 0 |
| 3 | 0.28 | 0.2 | 0.0479 | 0.4562 | 0.9358 | 0.0341 | 0.1454 | 0 |
| 4 | 0.1 | 0.4 | 0.017 | 0.0309 | 0.9209 | 0.0147 | 0.1182 | 0 |
| Yield, % | 98.3 | |||||||
| Purity, % | 94 | |||||||
| Cycle | tх | tу | Relative proportions of metals in 2 half period (organic phase) | |||||
| Ni | Cu | Fe | ||||||
| In | Out | In | Out | In | Out | |||
| 1 | 0.43 | 0.15 | 0.9887 | 0 | 0.9999 | 0 | 0.9839 | 0.0161 |
| 2 | 0.2 | 0.5 | 0.5041 | 0 | 0.9699 | 0.0163 | 0.1454 | 0.8384 |
| 3 | 0.28 | 0.2 | 0.0479 | 0 | 0.9356 | 0.0002 | 0.1182 | 0.0272 |
| 4 | 0.1 | 0.4 | 0.0166 | 0.0005 | 0.8976 | 0.0233 | 0.0077 | 0.1105 |
| 2 | 0.0001 | 0.9208 | 0 | 0.0077 | ||||
| Yield, % | 92.1 | 99.2 | ||||||
| Purity, % | 99.2 | 96.1 | ||||||
From the data presented in Table 3 it follows that with using 50 stages of the counter-current extraction for separation of three metals it is necessary to conduct four cycles, whereas in using 100 stages one cycle is enough for the complete separation of these metals (Table 2). In this case (N = 50), nickel flows out completely in the first half-period with the aqueous phase, while copper and iron come out with the organic phase to yield two fractions containing copper with a purity of 99.2% and iron with a purity of 96.1% (Table 3). Since the dimensionless sample loading time increases the productivity of the counter-current extraction process, effect of ts values on the yield and purity of metal separation was studied at N=50. Numerical studies (Table 4) showed that with increasing values of ts more cycles of the counter-current extraction are required to separate metals, while the yield and purity of separated metals remain relatively high.
Table 4. Effect of the dimensionless sample loading time (ts) on the yield and purity of metal separation (N = 50).
| ts | Number of cycles | Yield, % | Purity, % | ||||
|---|---|---|---|---|---|---|---|
| Ni | Cu | Fe | Ni | Cu | Fe | ||
| 0.01 | 4 | 98.3 | 92.1 | 99.2 | 94 | 99.2 | 96.1 |
| 0.2 | 4 | 95.3 | 92.5 | 98.1 | 98.3 | 97.8 | 95.9 |
| 0.4 | 6 | 97.5 | 84.2 | 98.8 | 96.3 | 95.8 | 92.7 |
| 0.5 | 7 | 96.4 | 80.1 | 97.8 | 94.3 | 80.1 | 87.8 |
Separation of four component mixtures
As mentioned above, the program can be used not only for the separation of binary mixtures but also for mixtures involving three and more components. In this section, using the program we consider the possibility of separating a mixture of four metals: nickel, copper, iron, and zinc. The total chromatogram (Figure 3b) was plotted on the basis of the results obtained for the binary mixtures (Figures 2a-2d).
In Table 5 there are the calculated results of the separation of four component mixture for one cycle. When the value of tx is equal to 0.58, during the first half-period of the first cycle nickel and zinc come out simultaneously with the aqueous phase, i.e., their separation is not observed. In the second period of the first cycle a mixture of four metals is separated, but yields of nickel and zinc are low (65.2 and 31.7%, respectively). When a value of tx is equal to 0.4, all the metals are completely eluted with the organic phase flows successively within one cycle but the purity of separated metals is less than in the previous case. Thus, varying values of tx and ty the separation of four component mixtures can be achieved.
Table 5. The calculation results of the separation of nickel, copper, iron, and zinc (KD: 0.57 (Cu), 0.20 (Ni), 1.27 (Fe), 0.11 (Zn); ts = 0.01; N = 100).
| tх | Relative proportions of metals in 1 half period (aqueous phase) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ni | Cu | Fe | Zn | ||||||
| In | Out | In | Out | In | Out | In | Out | ||
| 0.4 | 0.9999 | 0.0001 | 1 | 0 | 1 | 0 | 0.9993 | 0.0007 | |
| 0.58 | 0.6521 | 0.3479 | 0.9983 | 0.0017 | 1 | 0 | 0.3481 | 0.6519 | |
| Yield, % | 34.8 | 65.2 | |||||||
| Purity, % | 34.8 | 62.2 | |||||||
| tх | tу | Relative proportions of metals in 2 half period (organic phase) | |||||||
| Ni | Cu | Fe | Zn | ||||||
| In | Out | In | Out | In | Out | In | Out | ||
| 0.4 | 0. 5 | 0.9999 | 0 | 0.9419 | 0.0581 | 0.0142 | 0.9858 | 0.9993 | 0 |
| 1.5 | 0.9366 | 0.0634 | 0 | 0.9419 | 0 | 0.0142 | 0.9993 | 0 | |
| 2.8 | 0.0154 | 0.9212 | 0.9251 | 0.0742 | |||||
| 6 | 0 | 0.0154 | 0.0002 | 0.9249 | |||||
| Yield, % | 92.1 | 94.2 | 98.6 | 92.5 | |||||
| Purity, % | 93 | 92.3 | 94.4 | 98.4 | |||||
| 0.58 | 0.65 | 0.6521 | 0 | 0.9911 | 0.0073 | 0.025 | 0.975 | 0.3481 | 0 |
| 1.5 | 0.6521 | 0 | 0.0038 | 0.9873 | 0 | 0.025 | 0.3481 | 0 | |
| 4 | 0.0001 | 0.652 | 0 | 0.0038 | 0.3173 | 0.0308 | |||
| 6.5 | 0 | 0.0001 | 0.0004 | 0.3169 | |||||
| Yield, % | 65.2 | 98.7 | 97.5 | 31.7 | |||||
| Purity, % | 95 | 96.5 | 99.3 | 99.9 | |||||
Conclusion
The results presented in this paper showed using the calculation program [11] the separation of a given feed mixture of metals by the method of dynamic counter-current liquid-liquid extraction can be simulated for providing process intensification with remaining the selectivity. Numerical researches with using the experimental data on metal distribution coefficients demonstrate how proper selection of the operating conditions (parameters ts and number of cycles) can allow increasing the productivity by an order of magnitude ensuring, a desirable separation. It was shown that the program can be used not only for the separation of binary mixtures but also for mixtures involving three and four metals. For example, varying values of tx and ty the separation of three or four metal mixtures can be achieved in one technological operation.
Acknowledgments
This work was supported by the Russian Foundation for Basic Researches (project No. 15-03-02940).
References
- Belova VV, Kholkin AI. Binary extraction of platinum metals. Solvent Extr and Ion Exch. 1998;16(5):1233-55.
- Voshkin AA, Belova VV, Kholkin AI. Extraction of iron(III) by binary extractants based on quaternary ammonium bases and organic acids. Russ J Inorg Chem. 2003;48(4):608-13.
- Belova VV, Voshkin AA, Kholkin AI, et al. Solvent extraction of some lanthanides from chloride and nitrate solutions by binary extractants, Hydrometallurgy. 2009;97(3):198-03.
- Ito Y. Origin and evolution of the coil planet centrifuge. Sep Purif Rev. 2005;34(2):131-54.
- Kostanyan AE, Voshkin AA. Analysis of cyclical liquid chromatography. Theor Found Chem Eng. 2011;45(1):68-74.
- Kostanyan AE, Voshkin AA, Kodin NV. Controlled–cycle pulsed liquid–liquid chromatography.A modified version of Craig’s counter-current distribution. J Chromatogr A. 2011;1218(36):6135-43.
- Rubio N, Ignatova S, Minguillon C, et al. Multiple dual-mode countercurrent chromatography applied to chiral separations using a (S)-naproxen derivative as chiral selector. J Chromatogr A. 2009;1216(48):8505-11.
- Kostanyan AE. General regularities of liquid chromatography and countercurrent extraction. Theor Found Chem Eng. 2006;40(6):587-93.
- Hewitson P, Ignatova S, Sutherland IA. Intermittent counter-current extraction–Effect of the key operating parameters on selectivity and throughput. J Chromatogr A. 2011;1218(36):6072-78.
- Kostanyan AE, Erastov AA, Shishilov ON. Separation of liquid mixtures by dynamic countercurrent cyclic extraction. Theor Found Chem Eng. 2015;49(4):560-66.
- Kostanyan AE, Erastov AA, Shishilov ON. Multiple dual mode counter-current chromatography with variable duration of alternating phase elution steps. J Chromatogr A. 2014;1347:87-95.
- Kostanyan AE. Controlled cycle counter-current chromatography. J Chromatogr A. 2008;1211(1-2):55-9.
- Kostanyan AE. On influence of sample loading conditions on peak shape and separation efficiency in preparative isocratic counter-current chromatography. J Chromatogr A. 2012;1254:71-7.
- Marczenko Z. Spectrophotometric determination of elements. John Wiley and Sons, New York, 1986.