More on the orthogonal complement functions

Covariance structure analysis, Distribution free tests, Implicit function theorem, QR factorization.

Introduction

The orthogonal complement of a p×q matrix X with q<p and full column rank is a p×(p-q) matrix Y such that [X,Y] is invertible. Note that Y must have full column rank. Jennrich and Satorra in Theorem 1 show how to compute an orthogonal complement Y of an arbitrary p×q matrix X with full column rank q<p using the long form of a QR factorization. Unfortunately, Y is not a continuous function of X [1].

In a seminal paper Browne showed how to test the goodness of fit of an arbitrary covariance structure [2]. The proof of his main result Proposition 4 used a locally continuous orthogonal complement function, but because he failed to show such functions existed his proof was incomplete. In spite of the fact that his test had been used extensively this problem was not noticed until 2013 when Jennrich and Satorra pointed out that his proof was incomplete and completed it by showing that locally continuous orthogonal complement functions exist [1]. This was done using the implicit function theorem. A problem with the implicit function approach is that it does not give a formula for the function produced and Jennrich and Satorra conjectured their function could not be expressed by an explicit formula.

Browne and Shapiro say that this conjecture is incorrect by presenting an explicit formula for a locally continuous orthogonal complement function [3]. Browne and Shapiro in

slightly different notation state the following: Let X₀ be any p×q matrix with full column rank q<p and X^c₀ be any orthogonal complement of X₀. Consider the following matrix valued function:

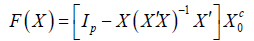
Let N be any neighbourhood of X₀ such that X has full column rank for all X ϵ N. Browne and Shapiro say that on N, F(X) is a well-defined continuous function and claim F(X) is an orthogonal complement of X for all X in N. They, however, fail to show this. In particular they fail to show F(X) has full column rank. As a consequence their claim is only a conjecture. We will begin by proving their conjecture.

Proof of the Browne-Shapiro conjecture

Lemma 1: Let X₀ be a p×q matrix of full column rank q<p. There is a neighbourhood N of X₀ that contains only full column rank matrices.

Proof: Let X be an arbitrary p×q matrix and let ɡ(X) =det(X'X ) . Since ɡ(X ) is continuous there is δ>0 such that

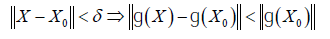
It follows from the last inequality that ɡ( X ) ≠ 0 and hence that det(X'X ) ≠ 0 and hence that X has full column rank for all X in the neighbourhood

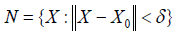
Lemma 2: Let X₀ be a p×q matrix with full column rank q<p and let X^c₀ be any orthogonal complement of X₀. Then

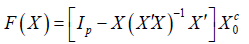
is continuous and well defined for X ∈ N .

Proof: By Lemma 1 all X ∈ N have full column rank. Thus F(X) is well defined. It follows from the continuity of matrix multiplication and matrix inversion that F(X) is continuous for all X ∈ N.

Theorem 1: Let X₀ be a p×q matrix with full column rank q<p. Let X^c₀ be any orthogonal complement of X₀. Then there is a neighbourhood N of X₀ such that X has full column rank for all X ∈ N and

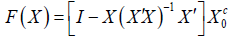
is an orthogonal complement of X.

Proof: Note that F(X) is p×(p-q) and F(X) is orthogonal to X. It is sufficient to prove F(X) has full column rank. Let ɡ(X ) =det(F(X )′F(X) ) . Then ɡ( X ) is a continuous and it follows from this that there is δ>0 such that

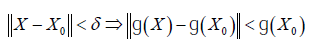
It follows from the last inequality that ɡ( X ) ≠ 0 . Hence det(F(X )′F(X) )≠ 0 and hence F(X) has full column rank.

This proof is much simpler than that given by Jennrich and Satorra using the implicit function theorem [1]. In their paper Browne and Shapiro prove Browne's Proposition 4 without using their F(X) formula. One could, however, use Theorem 1 because it asserts the existence of a locally continuous orthogonal complement function and this is all that is needed to fix Browne's proof of Proposition 4. There are now three proofs of Browne's Proposition 4, the one given by Jennrich and Satorra [1], the one given by Browne and Shapiro [3], and the one using Theorem 1.

A problem with using Theorem 1 is that for an X of interest one has no way of knowing if X is in N since the only thing we know about δ is that it is greater than zero. If necessary for an X of interest one can always compute an orthogonal complement of X using Theorem 1 of Jennrich and Satorra, but it will not be a continuous function of X [1].

See the following example which shows numerically that Theorem 1 of Jennrich and Satorra produces orthogonal complements as does Theorem 1 of this document and also suggests an interesting alternative method using F(X) [1].

Theory:

Example:

Let

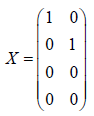
Then X is a p by q matrix with p = 4 and q = 2. Theorem 1 of Jennrich and Satorra [1] says that if

X= QR

is the long form of a QR factorization of X, then the last p-q columns of Q are an orthogonal complement of X. Computing a QR factorization of X gives

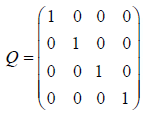
The last p-q columns of this are:

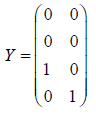
and this is an orthogonal complement X. This demonstrates numerically that Theorem 1 of Jennrich and Satorra [1] produces orthogonal complements.

Note that when X=X₀, X satisfies the assumptions of Theorem 1 and the computed value of

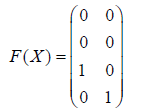
which is an orthogonal complement of X. Thus in this case at least F(X) is an orthogonal complement of X as asserted by Theorem 1.

Let

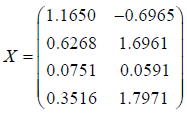
be a random matrix whose components are independent standard normal variables. Note that it has full column rank. The value of the Browne-Shapiro.

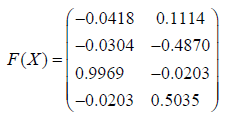
This has full column rank and hence is an orthogonal complement of X even though X may not satisfy the basic assumption of Theorem 1 above because X is simply a random matrix.

When this is repeated 1000 times in every case F(X) is an orthogonal complement of X. This suggests that F(X) is an orthogonal complement of X with high probability.

We show below that much more is true. We show F(X) fails to be an orthogonal complement of X only for X in subset of Labesgue measure zero in R^pxq.

Note that when X = X^c₀ , F(X)=0 and hence F(X) is not an orthogonal complement of X for all X with full column rank.

A necessary and sufficient condition for F(X) to be an orthogonal complement of X.

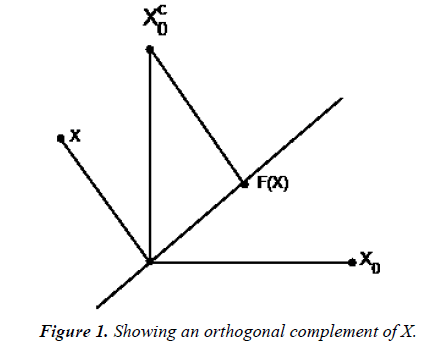
To simplify the development that follows let us begin by looking at the simplest possible case when p = 2 and q = 1. Assume X is not in the column space of X^c₀ . Then in Figure 1 clearly, F(X) is a non-zero vector and has full column rank. Thus F(X) is an orthogonal complement of X for all X not in the column space X^c₀ . If X is in the column space of X^c₀ , then F(X)=0 and hence F(X) is not an orthogonal complement of X. Note this happens only on a set that has Labesgue measure zero in R². We will show that this happens for arbitrary p by q<p matrices X.

Figure 1. Showing an orthogonal complement of X.

We begin with the following theorem,

Theorem 2: Let F(X) be the Browne-Shapiro formula. That [X,X^c₀] is invertible is a necessary and sufficient condition for F(X) to be an orthogonal complement of X.

Proof: Assume [X, X^c₀] has full column rank. Assume F(X) does not have full column rank. Then

F(X)a=0

for some vector a a ≠ 0. Thus

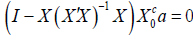
It follows that X^c₀a is in the column space of X. Thus

X^c₀a = Xb

for some vector b. Thus there is a vector in the column space of X that is in the column space of X^c₀ . It follows that [X, X^c₀] does not have full column rank. This contradiction proves F(X) has full column rank when [X, X^c₀] has full column rank. This is a sufficient condition for F(X) to be an orthogonal complement of X.

If [X, X^c₀] does not have full column rank, then Xa = X^c₀b for two vectors a and b not both zero. If a = 0, then b = 0. This implies a ≠ 0 which in turn implies b ≠ 0. Now

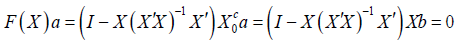
which implies that F(X) does not have full column rank. Thus F(X) is not an orthogonal complement of X when [X, X^c₀] does not have full column rank. Thus F(X) is an orthogonal complement of X if and only if [X, X^c₀] has full column rank.

How often does F(X) fail to be an orthogonal complement of X?

Lemma 2: A polynomial in n variables is either identically 0 or its roots have Labesgue measure zero in Rⁿ.

Proof: The proof is by mathematical induction on n. For n=1, P(x) of degree d can have at most d roots, which gives us the base case. Now, assume that the theorem holds for all polynomials in n-1 variables. Let 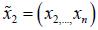and write

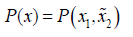
Let I[A] be the indicator function of a set A. By Fubini's theorem,

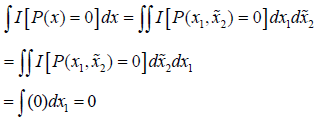
The first two integral equalities follow from Fubini's Theorem. The last integral equality follows from the fact that given is a polynomial in n-1 variables and by the induction hypothesis this is identically zero for all 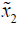or its zeros have Labesgue measure zero in R^n-1[4].

Comment: Lemma 2 is a simple very interesting result which apparently is not in the literature. It is not in any journals covered in Jstor. It is not in any of the five analysis books we own and according to Caron and Traynor it is not in any measure theory book.

Theorem 3: The X for which the Browne - Shapiro function F(X) is not an orthogonal complement of X have Labesgue measure zero in R^p×q.

Proof: F(X) is not an orthogonal complement of X if and only if [X, X^c₀] is singular. This happens if and only if det( [X, X^c₀][X, X^c₀])=0 . As a function of X this is not identically zero because it is not zero when X=X₀. Moreover det det( [X, X^c₀][X, X^c₀]) is a polynomial in p×q variables x=vec(X) which is not identically zero. It follows from Lemma 2 that its zeros have Lebesgue measure zero in Rpq. Or equivalently the X such that F(X) is not an orthogonal complement of X have Labesgue measure zero in R^p×q.

Remark: Theorem 3 implies that F(X) almost never fails to be an orthogonal complement of X. If X is a sample from a density, then F(X) is an orthogonal complement of X with probability one.

Conclusion

Browne and Sharpiro [3] give a formula for computing orthogonal complements. Let X₀ be any p×q matrix with full column rank q<p and X^c₀ be any orthogonal complement of X₀. Browne and Sharpiro function is

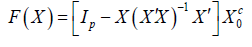
They state that if N be any neighbourhood of X₀ such that X has full column rank for all X ϵ N then F(X) is an orthogonal complement of X for all X in N. They, however, fail to show this. In particular they fail to show F(X) has full column rank. As a consequence their claim is only a conjecture. The main point of our paper is to prove their conjecture and much more. We prove that on all but a set of p×q matrices X with Labesque measure zero, F(X) is an orthogonal complement of X. In particular if X is a sample from a density, F(X) is an orthogonal complement of X with probability one.

Theorem 1 is a proof for the Browne-Sharpiro conjecture. We also prove additional results that should enhance considerably the practical relevance of the Browne-Shapiro function for an orthogonal complement. Theorem 2 gives a necessary and sufficient condition for F(X) to be an orthogonal complement of X. Lemma 2 is a not well known, but very useful result about the roots of an arbitrary polynomial in n variables. If the polynomial is not identically zero, its roots have Labesque measure zero. Theorem 3 is our main result.

Acknowledgements

The authors would like to thank Ellen Jennrich for proof reading our paper and helping with its submission. The research of the second author is supported by grant EC02014-59885-P from the Spanish Ministry of Science and Innovation.

References

1. Jennrich RI, Satorra A. Continuous orthogonal complement functions and distribution free goodness of fit tests for covariance structure analysis. Psychometrika. 2013;78: 445-552.
2. Browne MW. Asymptotically distribution-free methods for the analysis of covariance structures. Psychometrika. 1984;37: 62-83.
3. Browne MW, Shapiro A. A comment on the asymptotics of a distribution free goodness of fit test statistic. Psychometrika. 2013;78: 196-9.
4. Caron R, Traynor T. The zero set of a polynomial. 2005.