Research Article - Biomedical Research (2017) Volume 28, Issue 20
Medical image denoising based on dictionary learning
Xiao Chen1,2* and Qianli Shen1
1School of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, PR China
2Jiangsu Key Laboratory of Meteorological observation and Information Processing, Nanjing University of Information Science and Technology, Nanjing 210044, PR China
- *Corresponding Author:
- Xiao Chen
School of Electronic and Information Engineering
Nanjing University of Information Science and Technology, PR China
Accepted date: 29 December, 2017
Abstract
Images are widely used in medical engineering. Medical imaging devices are inevitable to introduce noises to medical images. It is important to eliminate noises in medical images. To denoise the images more effectively, this paper proposes an improved image denoising method based on dictionary learning. It introduced the image size and pixel distribution to define a new iteration more reasonably. When the iteration function is called, the threshold is properly compressed. The results show that the effect of dictionary updating is better, and that it improves the effect of noise reduction and greatly reduces the computing time consumed, in comparison to those of the KSVD and MOD algorithms. Therefore, it has the potential application value in medical image processing.
Keywords
Dictionary learning, Noise denoising, Threshold
Introduction
With the rapid medical development, medical images are more and more important in medical engineering [1-3]. When sharing of information such as image information and position information [4-6], devices are inevitable to introduce noises to medical images. It is important to eliminate noises in medical images. Image denosing based on dictionary learning is a new technology in image processing, which has become a hot research in image processing in recent years [7-12]. Compared to the traditional space, frequency domain, wavelet domain and other methods, the processing unit of dictionary learning method is more accurate, and the treatment effect is also improved. The traditional spatial and frequency domain and wavelet domain algorithm include median filtering, Wiener filtering, low-pass, high pass. These methods are often processed by image block approach to image processing. While, the dictionary learning method is mainly through point by image block processing.
The common dictionary learning methods are KSVD, MOD, K-means, and other methods. KSVD is a dictionary learning algorithm creating the dictionary by a singular value decomposition. MOD is one of the methods introduced to tackle the sparse dictionary learning. K-means is a method of vector quantization. These methods have been widely used. Sadeghi proposed a learning algorithm by Atomic Dictionary Based on noise reduction by using over complete dictionary [7]; Zongxu proposed a single image super-resolution method based on adaptive dictionary learning, using all kinds of dictionary in the comprehensive image reconstruction to determine the optimal dictionary [8]; Zemin et al. proposed a new algorithm of image denoising based on dictionary learning [9], learning the dictionary of the image features, image sparse representation. These dictionary learning algorithms need to determine the size of the dictionary in advance. However, in practical applications, the selection of the optimal value of the dictionary scale has no theoretical guidance. To denoise the images more effectively, this article proposes an improved image denoising method based on dictionary learning. It introduced the image size and pixel distribution to define a new iteration more reasonably. When the iteration function is called, the threshold is properly compressed. It improves the effect of noise reduction and greatly reduces the computing time consumed.
Method
The principle of dictionary learning [10-12] is
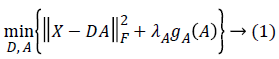
Here D is a dictionary (processing dictionary), X is a training set, A is a sparse matrix, λA is regularize parameters, and gA ( ) is the function of the sparsity of coefficients in the unified metric synthesis model. A dictionary is usually a multi-column matrix. Each column vector is a processed atom, which requires the D and A value corresponding to the minimum value of the expression.
In MDO (Method of optimal directions) method, the dictionary D is renewed
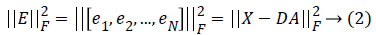
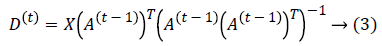
Here t is the number of iteration and A(t-1) is the matrix after t-1 times’ iteration.
The input image matrix is defined as y, which requires that the number of columns of the y must not be less than the number of the atoms in the dictionary. Then we define the size of the block_size, and regenerate the corresponding matrix of the generated noisy image with the im2col function into a matrix column, which is called image block variable patches, and the rearrangement way is sliding, that is, image block sliding and overlapping mode. The size function is used to measure the number and the number of columns of y. The number of rows is rows, the number of columns is cols, and then the dictionary A is constructed. The number of columns is the corresponding number of atoms in the column vectors mentioned above. Then the number of iterations is set up as the basis for the next dictionary update. To improve the iteration efficiency, a new iteration number is proposed. It not only improves the number of iterations, but also increases the accuracy of computation, and improves the adaptability of the algorithm.

Here iter_num is the number of iterations. It called the errGOAL function. There is an important value of errGoal, which is the maximum allowed error. The core function of errGoal is to build a sparse matrix. We extract the input image of the matrix corresponding to the number of columns and rows and dictionary D number of rows and columns respectively. There is a maximum threshold value maxnumcoef, which is defined as
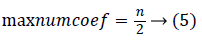
Here n is the number of rows of the corresponding matrix for the input image.
D’ is the transposing of D. It is assumed that

Then
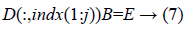
Here E is a unit matrix, and B is a required matrix. Because D is a sparse matrix, there is no reversible matrix. B is a pseudo reversible matrix. Then B*A is filled into the a. If the length of indx is greater than 0,
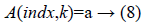
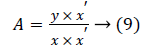
Here y is the input image matrix and x is a sparse coefficient matrix. Dictionary updates are made many times until each column of the matrix and less than the set threshold 10-7.
Defining reconstructed image block variables recpatches is
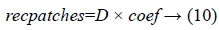
Here coef is a sparse matrix.
The number of columns of recpatches is extracted and recorded as ind. Then the image output variable is defined as imout and the weight variable is defined as weight. The size of the zero matrix is r × c (r, c, the length and height of the image matrix). Index values of expressions size(img)-block_size+1 are extracted. Row values and column values are stored in rows and cols respectively. Then the output of processing blocks is reconstructed, and the output of processing blocks is recorded. A cycle is set up, the cycle variable is i, the step is 1, and the cycle termination value is length(cols). The matrix is reorganized and reorganized. The recombined update is incorporated into the denoising process.
Each processing image block is obtained by dividing weight by the image output matrix imout,
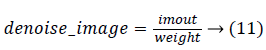
Finally, the local block of the denoised image is reorganized to form the denoising image.
Results
There are many indicators for image processing evaluation, such as PSNR, MSE, SSIM, MAE. In terms of denoising, PSNR is one of the most important indicators.
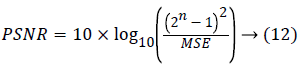
Here MSE is a mean square error. MAE mean absolute error is
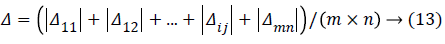
That is to add the difference for each pixel. In this equation, m and n are the size of the image.
This paper used the classic 256 test image lena.bmp, cameraman.tif, and rice.png [2] in the experiments. Table 1 is the comparison results of the above images by using MOD, KSVD and the presented method. The average SSIM of KSVD is 0.8853, MOD is 0.8816, and proposed is 0.88. Table 2 shows the PSNR comparison by using the three methods.
| Rice.png | Cameraman.tif | Lena.bmp | ||
|---|---|---|---|---|
| KSVD | SSIM | 0.9293 | 0.8427 | 0.8840 |
| MAE | 6.1317 | 6.1130 | 6.1143 | |
| MOD | SSIM | 0.9269 | 0.8358 | 0.8823 |
| MAE | 6.2979 | 6.1407 | 6.1514 | |
| Proposed | SSIM | 0.9255 | 0.8381 | 0.8764 |
| MAE | 6.4016 | 6.2708 | 6.2047 |
Table 1. Comparison of the above images by using MOD, KSVD and the proposed method.
| Cameraman | Lena | Rice | |
|---|---|---|---|
| KSVD | 36.8018 | 50.0742 | 53.4228 |
| MOD | 36.9454 | 50.4352 | 55.1204 |
| Proposed | 54.5545 | 50.4352 | 54.8721 |
Table 2. PSNR comparison by using the three methods.
Discussion
From Table 1, random noises are also added to the original images and the results of MOD and KSVD are different from that of the improved method. Compared with MOD and KSVD method, the improved method has better treatment effect. It is mainly reflected in the degree of clearness and detail protection of denoising map, and the image and texture of the improved method are more detailed, the outline is more prominent, and the grayscale distribution is more reasonable. The SSIMs of all the images are almost the same as those of KSVD and MOD. It shows that the improved method is better in detail fidelity and noise elimination while denoising. From a visual point of view, the clarity of the improved method is also better than the KSVD and MOD methods. For Lena.bmp, the face contour is better and clearer. As for cameraman.tif, the contrast between the photographer's profile and the background is better than the KSVD and the MOD methods. As for rice.png, the characteristics of rice grains are better and clearer.
Table 2 shows the PSNR comparison by using the three methods. From Table 2, The PSNR of the improved method is higher than the PSNR values of KSVD and MOD methods. The average PSNR is 17.2% more than that of the KSVD and 15.7% more than that of MOD. It shows that the denoising performance of the improved method is better, and the image enhancement effect is obvious. Dictionary learning involves a large number of computing. Therefore, dictionary learning time is much consumed. For this purpose, MATLAB is used to measure the time consumption of three methods. In our test, the computing time of KSVD is 833.9s, that of MOD is 706.7s, and that of the proposed method is 148.0s. The time of the proposed method was much smaller than those of KSVD and MOD methods, reflecting the proposed method of computational complexity and computational advantages and characteristics of the times in reducing.
Conclusion
This paper proposes an improved image denoising method based on dictionary learning. It introduced the image size and pixel distribution to define a new iteration more reasonably. When the iteration function is called, the threshold is properly compressed. The accuracy of the dictionary is better, which makes the image denoising more accurate. To sum up, the improved method indeed improves the integrity of the denoising and the details of the fidelity, and has the value of medical application.
Acknowledgment
This work was supported in part by project grants from the six talent peaks project in Jiangsu Province (DZXX-006), in part by 333 high level personnel training project Jiangsu Province of China, in part by the Natural Science Foundation of Jiangsu Province of China (BK20161536), and in part by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References
- Chen X, Hu C. Medical image encryption based on multiple chaotic mapping and wavelet transform. Biomed Res India 2017; 28: 8834-8837.
- Chen X, Hu C. Adaptive medical image encryption algorithm based on multiple chaotic mapping. Saudi J Biol Sci 2017; 24: 1821-1827.
- Chen X, Ji Q, Xu C. Effect of load on shear wave speed in muscle. Biomed Res 2017; 28: 8985-8987.
- Chen X, Zou S. Improved wi-fi indoor positioning based on particle swarm optimization. IEEE Sensors J 2017; 17: 7143-7148.
- Chen X, Zhang B. 3D DV-hop localisation scheme based on particle swarm optimisation in wireless sensor networks. Int J Sensor Networks 2014; 16: 100-105.
- Chen X, Zhang B. Improved DV-hop node localization algorithm in wireless sensor networks. Int J Distributed Sensor Networks 2012.
- Sadeghi M, Babaie-Zadeh M. Learning overcomplete dictionaries based on Atom-by-atom updating. IEEE Transact Signal Process 2014; 62: 883-891.
- Pan Z, Yu J, Xiao C. Single image super resolution adaptive dictionary based on learning algorithm. J Electronics 2015; 43: 209-216.
- Cai Z, Lai J. A method for image denoising based on dictionary learning. J Electronic 2009; 37: 347-350.
- Tang H, Zhang X, Chen H. The incoherent dictionary learning method with boundary condition constraints and its sparse representation. Automation J 2015; 41: 312-319.
- Shi J, Wang X. Reconstruction of super-resolution image based on improved K-SVD dictionary learning. J Electronic 2013; 41: 997-1000.
- Jia K, Wang X, Tang X. Image transformation based on learning dictionaries across image spaces. IEEE Transact Pattern Anal Machine Intel 2013; 35: 367-380.