Journal of Biochemistry and Biotechnology

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Review Article - Journal of Biochemistry and Biotechnology (2017) Industrial Biotechnology

Kinetic models for biomass pyrolysis.

Teresa Martí-Rosselló, Jun Li*, Leo Lue

Department of Chemical and Process Engineering, James Weir Building, 75 Montrose Street, University of Strathclyde, Glasgow G1 1XJ, UK

Corresponding Author:
Dr. Jun Li
Department of Chemical and Process Engineering
University of Strathclyde
United Kingdom
E-mail: jun.li@strath.ac.uk

Accepted Date: December 06, 2016

Citation: Martí-Rosselló T, Li J, Lue L. Kinetic models for biomass pyrolysis. Arch Ind Biotechnol. 2016; 1(1): 4-7

Visit for more related articles at Journal of Biochemistry and Biotechnology

Abstract

Biomass can be thermally treated to generate a wide range of valuable products, which can be used as a fuel or for chemicals production. Pyrolysis is a popular thermal process that is used to transform biomass into either bio-oil or bio-char by controlling the operating conditions (e.g., temperature and residence time); however, because biomass is a highly heterogeneous material, its pyrolysis involves complex chemical and physical changes. Various proposed mechanisms have been successful in capturing different aspects of biomass pyrolysis in different conditions, but there is still lack of consensus on a definitive kinetic mechanism. This review summarizes and discusses different types of kinetic models used to describe biomass pyrolysis and predict product yields.

Keywords

Biomass, Kinetic model, Pyrolysis.

Introduction

Biomass is a versatile material. It can be directly combusted to produce heat; however, by first subjecting it to a thermal or biological degradation, it can also be converted to products with a higher heating value or to materials with properties superior to those of the raw material [1]. When heated in the absence of oxygen, biomass decomposes into a range of products; including char (solid), tar (liquid) and gas; each with properties that differ from the raw biomass. Pyrolysis is considered to occur in two stages: primary decomposition of biomass and secondary reactions of the products generated in the primary decomposition. In order to maximize tar production, the volatiles released from the primary decomposition should be removed from the reaction zone and condensed before the secondary reactions occur, otherwise the volatiles will react further to form more gas and char. The thermal conversion of biomass is affected by heat and mass transfer, reactor configuration and the operating conditions that define the process environment, but the underlying reaction kinetics are key to describing, optimizing and scaling-up the process. Many studies have been undertaken to understand the kinetics of biomass pyrolysis; however, due to the heterogeneity of biomass and the complexity of the chemical and physical changes that occur during pyrolysis, it is difficult to develop a simple kinetic model that is applicable in every case. As a result, this field is still an active area of research. In this review, different methods to describe biomass pyrolysis and different types of kinetic mechanisms are discussed. Other up to date reviews on the subject with different scopes can be found in the literature [2,3].

Kinetic Models

In order to experimentally determine the kinetic parameters of biomass pyrolysis, there are isoconversional methods or model fitting methods. The main difference between isoconversional and model fitting methods is that the former does not assume any model to calculate the kinetic parameters, whereas the latter determine the kinetic parameters using a mass dependent function. Model fitting methods can be classified as onecomponent or multi-component according to how the initial biomass is characterized (e.g., specific type of biomass or by its components); and as lumped or detailed reaction mechanisms depending on how the products are defined (by lumped products such as gas, char and tar or by species in each lumped product) [3]. The distributed activation energy models (DAEM) differ from the previous models in that for each reaction, an activation energy distribution is used instead of a single value.

Biomass pyrolysis is normally experimentally studied with thermogravimetric analysis (TGA). TGA is used to determine the proximate characterization (moisture, volatile content, fixed carbon and ash) of the biomass and to study its pyrolysis kinetics. TGA measures the weight change of a biomass sample under isothermal conditions, where the decomposition is studied as a function of mass loss versus time, or non-isothermal conditions, as a function of mass loss versus temperature. Normally, intrinsic kinetic parameters are obtained from thermogravimetric experiments performed with low heating rates up to 100 K/min [4] and with fine particles below 1 mm, to produce a kinetically controlled regime [5,6]. Intrinsic parameters are scale independent and do not include the effect of transport phenomena, which make them more reliable for scaling up and reactor design. With high heating rates and large particle sizes, thermal gradients are observed and the process becomes no longer kinetically controlled, but diffusion limited [7]. The experimental conditions are not the same as for industrial applications, therefore, the kinetic parameters are not reliable for extrapolation [4].

All pyrolysis models describe the process in the form of mathematical expressions, which can be based on experimental data (empirical model) or on the relationship and behavior of the system components (mechanistic model). Biomass pyrolysis, would ideally be described by a mechanistic model, but developing a rigorous mechanistic model would be impractical or impossible [8]. That is the reason why most biomass pyrolysis models can be categorized as pseudo-mechanistic, since they make assumptions about the underlying chemistry but their kinetic parameters are fit to experimental data.

In order to describe biomass pyrolysis kinetics from thermogravimetric data, there are isoconversional or model free and model fitting methods [9]. For isoconversional methods, several TGA experiments at different temperatures or heating rates are required for the same value of conversion (mass loss), in order to obtain the apparent activation energy as a function of conversion. The advantage of isoconversional methods is that a reaction model that describes the process is not needed [10]. However, a proper reaction mechanism offers a closer approach to the intrinsic kinetics of the process [11]. An isoconversional approach can avoid problems related to the uncertainty of determining a specific reaction mechanism before analyzing the kinetic parameters [12], and mechanistic conclusions about the model could be drawn after the activation energy has been determined. The downsides of this method are the elevated number of experimental thermogravimetric runs, that the rest of kinetic parameters cannot be directly calculated [12], and that the kinetics elucidated are apparent parameters without a mechanistic interpretation [13]. It is recognized, though that with diverse runs of thermal analysis, both isoconversional and model fitting methods can produce valid kinetic parameters [8].

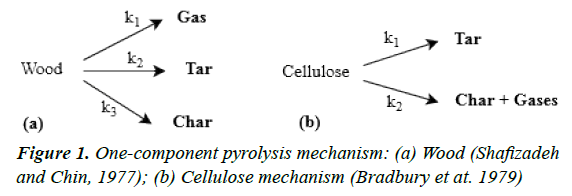
Model fitting methods, such as single or multiple reaction models and distributed activated energy models are widely used to describe biomass pyrolysis. In these methods, a kinetic mechanism is assumed. A kinetic mechanism describes a reaction process in one or several steps, each of them having specific temperature-dependent kinetic parameters (e.g., following the Arrhenius equation). The first kinetic mechanisms used for biomass pyrolysis are based on the primary decomposition of a specific type of biomass; therefore, they are not generalizable to other types of biomass, since the initial composition of the biomass strongly affects its pyrolysis performance [14]. Figures 1a and 1b show examples of this type of kinetic model. Both models feature competitive parallel reactions, and the product yields depend on the operating conditions, such as heating rate and final temperature. The global rate constant k is the sum of all the individual rate constants.

archives-of-industrial-biotechnology-pyrolysis-mechanism

Figure 1: One-component pyrolysis mechanism: (a) Wood (Shafizadeh and Chin, 1977); (b) Cellulose mechanism (Bradbury et at. 1979)

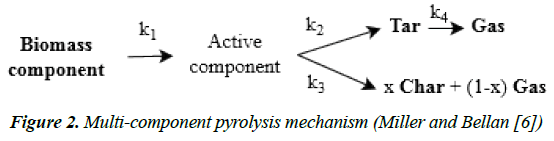
Kinetic models based on the “summative” principle are generalizable to a wider range of biomass [15] in which the overall decomposition of biomass is the weighted sum of the individual decomposition of its three main components, i.e. cellulose, hemicellulose and lignin. Therefore, a combination of the individual mechanisms of its main components is used, each mechanism with a specific set of kinetic parameters. The multi-component mechanism is suitable for a wide range of biomass as long as the biomass is properly characterized, since the amount of its components is the starting point for the process analysis. For this mechanism, it is typically assumed that no interaction occurs between the components during pyrolysis. Figure 2 presents an example of such a kinetic model; it also includes an intermediate step leading to the formation of an active component, which is believed to have the same chemical properties as the initial component but with modified physical properties, such as porosity [3]. These pyrolysis mechanisms are able to describe the different product yields in a lumped manner. To predict the product yields from secondary pyrolysis, reactions of the volatile in the gas phase before condensing to tar should be taken into account (see reaction 4 in Figure 2).

archives-of-industrial-biotechnology-Multi-component

Figure 2: Multi-component pyrolysis mechanism (Miller and Bellan [6])

The active component is currently used in most of the kinetic mechanisms; however, a reversible behavior of the active cellulose under 260°C has been observed [16,17], and a model for cellulose decomposition, which includes the step of active cellulose in competition with direct decomposition of cellulose to volatile, has been suggested [18].

In order to predict the product composition, and not only the lumped product yields, a more detailed mechanism is required [19,20]. This multi-component comprehensive mechanism is developed at a particle scale, and can be used for different reactor types with a wide range of operating conditions. An example of the detailed cellulose mechanism is found in Figure 3.

archives-of-industrial-biotechnology-Cellulose-decomposition

Figure 3: Cellulose decomposition mechanism (Ranzi et al. [18])

The distributed activation energy model [21,22] was firstly applied for coal [23] and later adapted for biomass [24]. This model can predict, in a lumped manner, the volatile release from biomass pyrolysis, assuming that the process complexity can be described using a distributed activation energy. The activation energy can follow a Gaussian, Weibull or Gamma distribution [25]. This distributed activation energy would represent a large number of parallel reactions, each of them with their own preexponential factor or sharing the same one in order to have a continuous distribution of activation energies [26]. DAEM can also be used with three independent reactions corresponding to cellulose, hemicellulose and lignin, having each of them their own distribution of activation energy [27]. DAEM is considered to be the most accurate and reliable of the pseudo-mechanistic approaches for biomass pyrolysis [28,29]. Some variations of the model, such as a temperature dependence of the pre-exponential factor [30] and a double distribution of the activation energy to account for the pyrolysis secondary reactions [31-37] have been suggested.

Conclusion

Overall, different mechanisms have been successful in capturing various aspects of the biomass pyrolysis in different conditions; however, there is still no consensus on a definitive kinetic mechanism. The multi-component mechanism is useful when considering mostly lignocellulosic biomass, but other components, like extractives and inorganic components, might also have a significant role on pyrolysis of biomass. There is still room for improvement in developing kinetic models able to describe biomass pyrolysis for a wider range of operating conditions, since the kinetic parameters obtained are often suitable only for a certain range of temperatures. Improving the mechanisms in terms of predicting the product yields and composition, suitability for a wider range of biomass and operating conditions are imperatives to consider in future kinetic models. Nevertheless, the final choice of a mechanism will always depend on the aim of the study, since more detailed mechanisms entail also an increase in complexity of the analysis.

References

Get the App