Review Article - Journal of Chemical Technology and Applications (2017) Volume 1, Issue 1
Development of an optimal control scheme for the process of epoxy resins modification with a complicated mathematical model in the control loop.
Sharikov FI, Sharikov IV*
Saint Petersburg Mining University, Russia
- *Corresponding Author:
- Sharikov IV
Saint Petersburg Mining University, Russia
Tel: +7-911-213-15-96
?-mail: yvshar@mail.ru
Accepted date: September 07, 2017
Citation: Sharikov FI, Sharikov IV. Development of an optimal control scheme for the process of epoxy resins modification with a complicated mathematical model in the control loop. J Chem Tech App. 2017;1(1):1-6.
DOI: 10.35841/chemical-technology.1.1.1-6
Visit for more related articles at Journal of Chemical Technology and ApplicationsAbstract
The problem of optimal control for a highly exothermal technological process with distributed state variables and with a large dead time is discussed. The main steps of creating a flexible control system with using the object model in the control loop are considered. It is shown that heat flux calorimetry is an effective experimental technique for the development of a process model based upon corresponding multistage kinetic model. It can be also applied to multiphase reaction systems together with simplified hydrodynamic models for mass transfer phenomena description. A successful application of this approach for developing the process mathematical model and its further introduction to the corresponding control system has been demonstrated for an important industrial process ? modification of epoxy resins with butanediol-1,4 for further synthesis of epoxy-urethane polymers with improved physico-chemical and mechanical properties. The process mathematical model makes it possible to specify the optimal operating mode for each resin and implement the optimal control.
Keywords
Mathematical modeling, Chemical kinetics, Calorimetry, Control model, Object with delay, Epoxy resin.
Introduction
The necessity to create complicated models of industrial processes with a high predictive capability for various purposes that can be used in a number of situations is widely discussed in the literature [1-5]. These models are increasingly becoming to penetrate to customized control interfaces and sometimes make it possible to provide an advice for a complex decision even without any detailed information about the underlying technology [1].
Modeling with a high-fidelity prediction can obviously provide a new significant value, and in order to realize this value one needs to make an effort in modeling as well as to perform a necessary amount of experimental study. One of the remaining challenges is also to persuade the process industry management and the technical personnel engaged in modeling and around, to broaden their perceptions of the future possible benefits [1].
An adequate model can sometimes be applied to explore a much wider design territory than is usually possible via traditional experimentation or constructing pilot plants, and it may be done in a much shorter time period. Hence, the modelbased engineering approach can generate the new important information that is simply not available via other techniques. The risk at developing a new technology as well as pilot plant testing period can also be considerably reduced in this case [1- 4]. It is especially vital when we deal with a flexible or multiassortment technology.
Developing an appropriate process control system is a key part of the general model-based engineering approach mentioned above [5,6]. Closed control systems based upon monitoring deviation with a feedback loop are widely used in industry for various technological objects [7-13]. However, they often cannot be successfully used for controlling an object with distributed state variables and with a large dead time – e.g., large tubular and batch reactors, shell tubular heat exchangers, distillation columns and so on – in case of supporting a control variable at the output of the apparatus [14,15]. Besides, a control system via deviation usually cannot be used in case of a potentially dangerous object, as deviation of regulation parameters from the given values in this case is not permitted from the viewpoint of the process safety [15,16].
Formulation of the optimal control task
In case of an object with distributed parameters one should use a predicative control system which is able to generate control actions in order to provide the corresponding compensating actions for input disturbances while the process is run through a regulating channel. Generation of such control signals is based upon analysis of the object input variables and an exact algorithm of input variables transformation into output variables. In this case it is possible to use calculation methods that take into account transfer functions of passing a disturbance through regulation channel [13-15]. In these cases a control system may generate the necessary control actions that should support regulated values at the given level. If we use a computer in the control loop it is possible to use a mathematical model of the object for predicting the object behavior in case of input disturbances. In this case the control system may be called the “control system with a fast model” in the control loop. Due to this solution a mathematical model of the object makes it possible to obtain an object response faster than the real object response, and it is possible to analyze it and to generate an optimal control action in order to compensate any possible deviations of regulated variables from the set points.
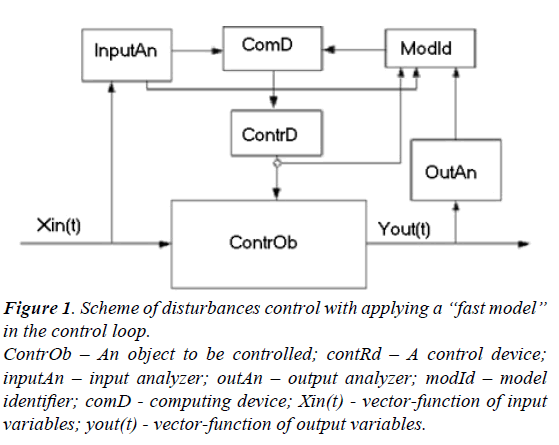
A principle scheme of the control system with a “fast model” in its control loop is given in Figure 1.
Figure 1: Scheme of disturbances control with applying a “fast model” in the control loop.
ContrOb – An object to be controlled; contRd – A control device; inputAn – input analyzer; outAn – output analyzer; modId – model identifier; comD - computing device; Xin(t) - vector-function of input variables; yout(t) - vector-function of output variables.
ContrOb – An object to be controlled; ContrD – A control device; InputAn – Input analyzer; OutAn – Output analyzer; ModId – Model identifier; ComD - Computing device; Xin(t) - Vector-function of input variables; Yout(t) - Vector-function of output variables.
Input variables are passed through the device InputAn –input analyzer. After that the vector of input parameters and the vector of input disturbances both proceed to a computing device ComD and also to ModId – model identifier. The information about current values of the control vector parameters comes to ModId as well. An inverse task is solved in ModId and current parameters of the mathematical model are specified in the result. The time delay value should be taken into account for every signal. It is a very important step of the whole identification procedure. The real time delay values may be either specified or measured directly in special experiments. In this case the typical preset disturbances are acted on the object. Analyzing the result of these disturbances one can specify the exact values delay time value for every control channel.
After its identification the model is transferred to a computer device where the optimal control action values are calculated. These optimal control action values correspond to the current state of a controlled object. At present such control schemes are used to control some complicated processes characterized by variegated disturbances of input variables. On the base of available experience to control the systems of a kind it is possible to specify the critical deviation state variables that should be identified through the mathematical model. This procedure allows to fulfill the identification procedure not very often and to raise the processing speed of the control system.
Creating models for control systems
Process systems are often described in terms of a mixed set of integral, partial differential and algebraic equations (IPDAEs), and this is the usual presentation of most established software tools designed for process systems engineering [1,8]. IPDAE systems are usually reduced into a mixed set of ordinary differential and algebraic equations, or DAEs. Ordinary differential equations (ODEs) typically arise from the conservation of fundamental quantities of nature, and algebraic equations (AEs) result from processes where accumulation is not important or transients are considered to occur instantaneously, and also by introduction of some auxiliary relationships between the variables [1].
Discontinuities in the governing phenomena of a chemical system usually arise from thermodynamic, transport, and flow transitions and also structural changes in the control configuration. Some of these transitions are reversible symmetric or asymmetric discontinuities, others are irreversible discontinuities. Another kind of discontinuities arises from external actions imposed by the surroundings on the system at a particular point in time, typically discrete manipulations and disturbances such as operating procedure or imposed failures [1].
The ability to incorporate complex sets of discontinuities describing a series of states in the formulation of a DAE system leads to the concept of state-task networks (STNs) [1,8]. Most modern custom-developed modeling tools are capable to solve complex problems that involve various combinations of DAE and STN systems.
At creating models for control systems it is very important to predict the object performance in a wide interval of changing the variables. The models based upon chemicals kinetics and hydrodynamics equations of an object are very perspective in this case. A number of well-known simplified hydrodynamic models are commonly used, such as an ideal mixing model, a plug flow model and some combinations of these models. As for kinetic models – the models based upon DSC, TG/DSC and heat flux calorimetry data are very promising. These experimental techniques are widely used for the study and characterization of epoxy resins reactivity [17-20].
The use of calorimetry for kinetic study and modeling is based upon the fact that overall heat generation rate is connected with the chemical reaction rates as follows:
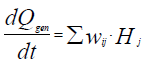 (1)
(1)
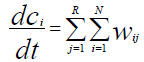 (2)
(2)
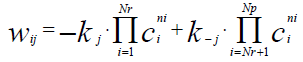 (3)
(3)
Where
Qgen\kJ – Total amount of heat generated or absorbed in a chemical process;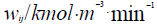 – reaction rate of the i-th component of reaction mixture in the j-th chemical reaction;
– reaction rate of the i-th component of reaction mixture in the j-th chemical reaction;
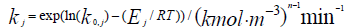 - Rate constant of a direct reaction;
- Rate constant of a direct reaction;
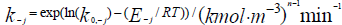 - Rate constant of an inverse reaction;
- Rate constant of an inverse reaction;
n - Order of a reaction;
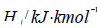 – Heat effect of a chemical reaction;
– Heat effect of a chemical reaction;
t/min – Current time of the process.
The procedure that is usually used for kinetic parameters determination from the experimental data is based upon searching the kinetic parameters to agree the condition of a minimal mismatch between the experimental data and the process modeling results. The sum of deviation squares between experimental data and modeling results is usually used as a measure of such mismatch in accordance with the equation (4):
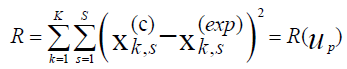 (4)
(4)
Where:
k - Index of a time point on a kinetics curve;
s - Index of a measured state variable in a kinetics experiment;
c - Calculated data;
exp - Experimental data;
K - Number of experimental points of a kinetics curve;
S - Number of the measured state variables of a mathematical model;
up – The required kinetics parameters (pre-exponential factors, activation energies, reaction orders, heat effects).
Various nonlinear programming methods are used at searching the extremum. Calculated data values and state variables are generated through numerical solution of the mathematical model differential equations with applying the Runge-Kutta method or LSODA method [21,22].
Results and Discussion
Modeling the process of epoxy resin modification with 1,4-butanediol
Modification of epoxy resins with butanediol-1,4 alcohol is chemical process that has been discussed and verified with the proposed approach. Modification is a powerful instrument for expanding the functionality and improving physical and mechanical characteristics of final polymers or polymer coatings [17,18]. Kinetic study of modification reactions of chlorine containing epoxy resins was done with the use of heat flux calorimetry. C80 Calvet calorimeter (SETARAM Instrumentation) was applied. Heat generation rate curves were taken as experimental responses together with the analysis result data in final points. The following kinetic scheme has been proposed for the modification process [21]:
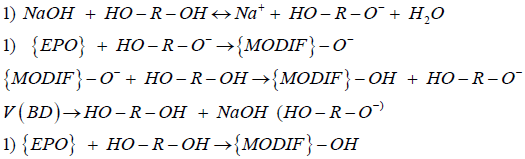 (5)
(5)
The process mathematical model has been developed on base of a kinetic study in the form of the following system of differential equations:
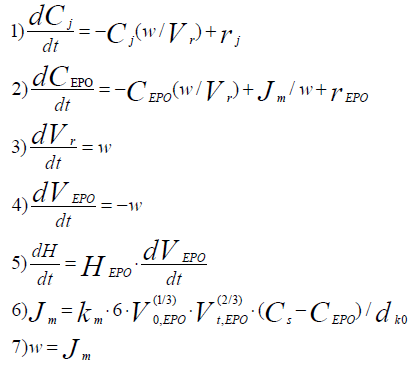 (6)
(6)
Where:
Ci /kmolm-3 – concentrations of all components of the reaction mixture except for concentration epoxy groups;
?EPO/kmolm-3 – Epoxy groups concentration in the reaction phase;
Vr/m3 – Volume of reaction phase;
VEPO/m3 – Volume of epoxy resin in the reactor;
Jm/kmol·m-3 – Mole flow of epoxy groups in the reaction phase;
v/m3·s-1 – Volume flow in the reaction phase;
ddr,0/m – Drop volume of dissolving phase at initial time moment;
dEPO/kmol·m-3 – Mole density of an epoxy group.
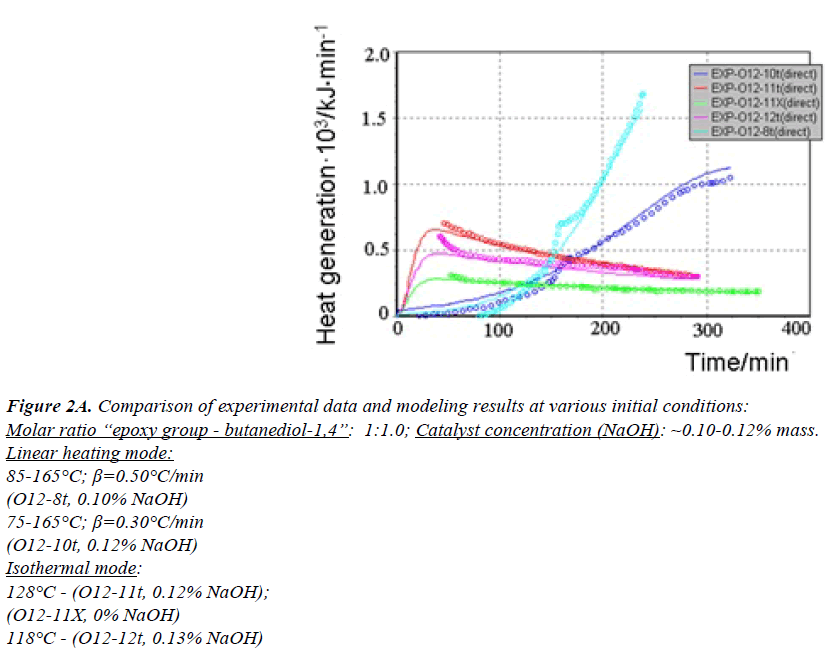
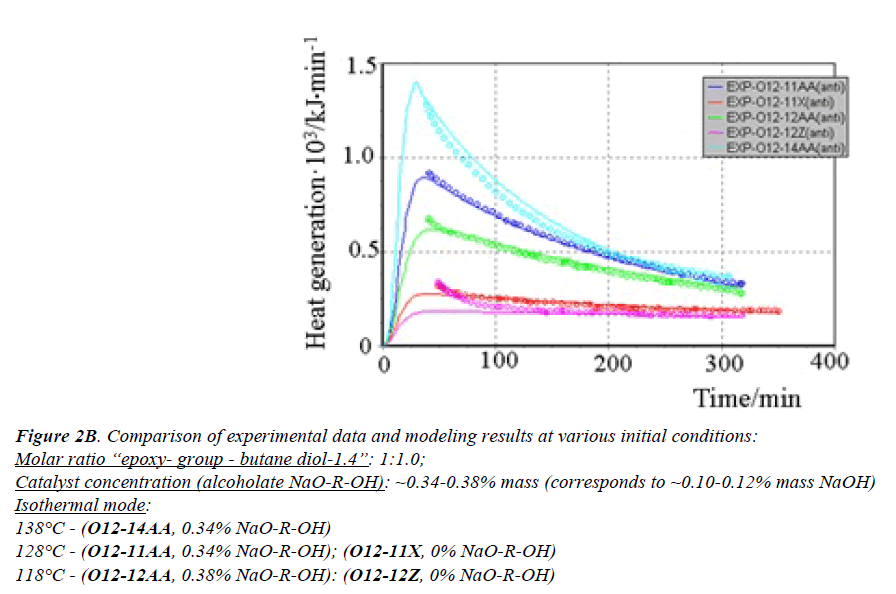
All generated heat is distributed uniformly between the phases and heat exchange is not taken into account. ReactOp Cascade 3.20 program package was used for solving the inverse kinetic task [22,23]. Comparison of experimental data and modeling results is presented in Figures 2a and 2b.
Figure 2A: Comparison of experimental data and modeling results at various initial conditions:
Molar ratio “epoxy group - butanediol-1,4”: 1:1.0; Catalyst concentration (NaOH): ~0.10-0.12% mass.
Linear heating mode:
85-165°?; β=0.50°?/min
(O12-8t, 0.10% NaOH)
75-165°?; β=0.30°?/min
(O12-10t, 0.12% NaOH)
Isothermal mode:
128°? - (O12-11t, 0.12% NaOH);
(O12-11?, 0% NaOH)
118°? - (O12-12t, 0.13% NaOH)
Figure 2B: Comparison of experimental data and modeling results at various initial conditions:
Molar ratio “epoxy- group - butane diol-1.4”: 1:1.0;
Catalyst concentration (alcoholate NaO-R-OH): ~0.34-0.38% mass (corresponds to ~0.10-0.12% mass NaOH)
Isothermal mode:
138°? - (O12-14AA, 0.34% NaO-R-OH)
128°? - (O12-11AA, 0.34% NaO-R-OH); (O12-11?, 0% NaO-R-OH)
118°? - (O12-12AA, 0.38% NaO-R-OH): (O12-12Z, 0% NaO-R-OH)
Optimization of the epoxy resin modification process
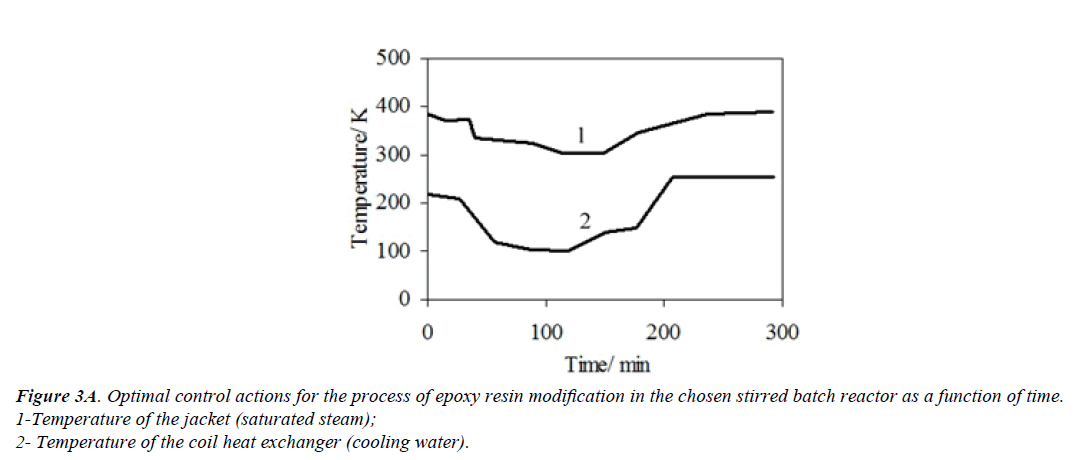
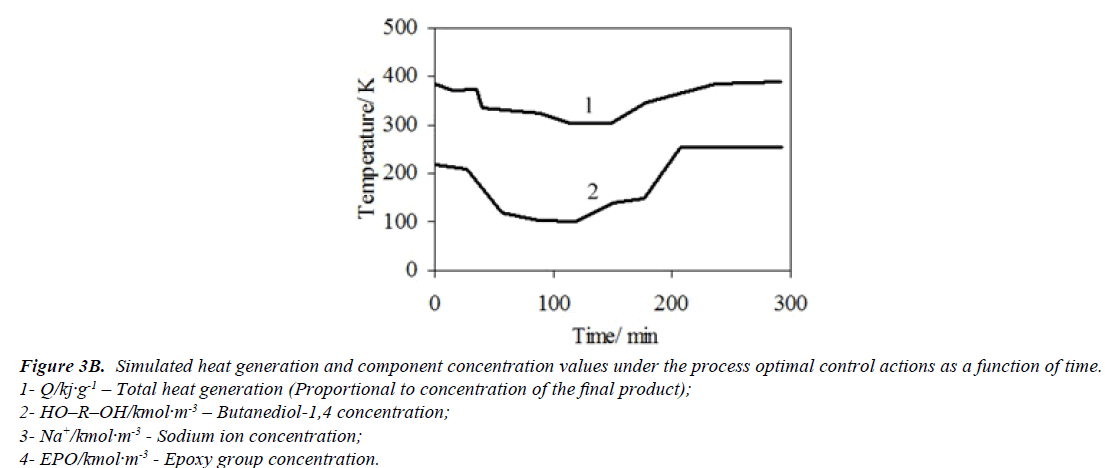
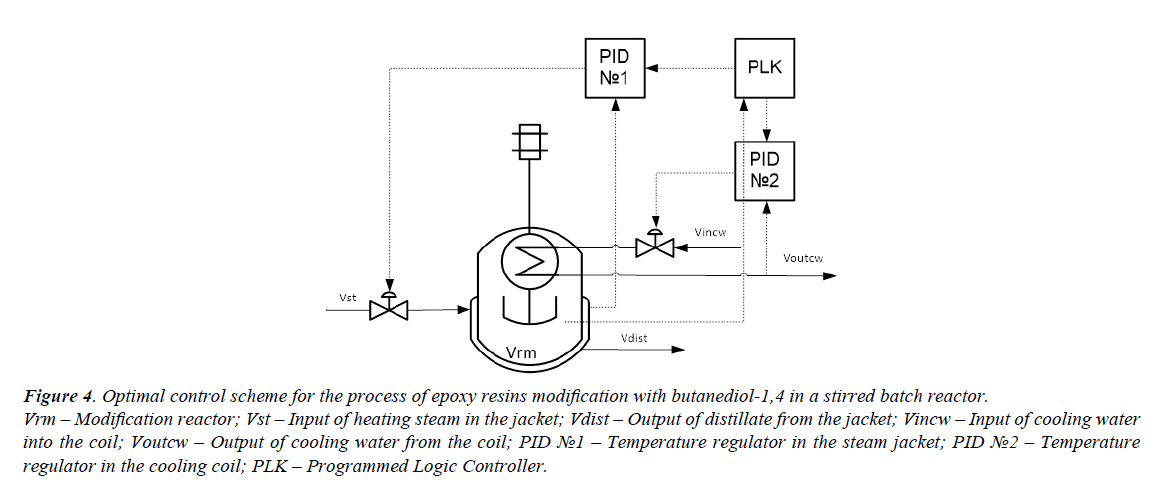
An optimal temperature profile for the chosen chemical reactor should provide a maximal concentration of the final product (modified epoxy groups) at the end of the process. Temperatures of heat exchange facilities (temperatures of cooling water and heating steam) were chosen as control actions. These control actions should provide an implementation of the optimal temperature profile with taking into account the disturbances. The values of optimal control actions in the control loop, calculated with the mathematical model in block ComD are given in Figures 3a and 3b. These control actions are transferred to the controller unit. The proposed control scheme is given in Figure 4.
Figure 3B: Simulated heat generation and component concentration values under the process optimal control actions as a function of time.
1- Q/kj·g-1 – Total heat generation (Proportional to concentration of the final product);
2- HO–R–OH/kmol·m-3 – Butanediol-1,4 concentration;
3- Na+/kmol·m-3 - Sodium ion concentration;
4- EPO/kmol·m-3 - Epoxy group concentration.
Figure 4. Optimal control scheme for the process of epoxy resins modification with butanediol-1,4 in a stirred batch reactor. Vrm – Modification reactor; Vst – Input of heating steam in the jacket; Vdist – Output of distillate from the jacket; Vincw – Input of cooling water into the coil; Voutcw – Output of cooling water from the coil; PID ?1 – Temperature regulator in the steam jacket; PID ?2 – Temperature regulator in the cooling coil; PLK – Programmed Logic Controller.
Conclusions
1. Analysis of the control problem for a complicated technological process with a considerable heat generation/consumption has been carried out.
2. An experimental technique based upon heat flux calorimetry and kinetic modeling has been proposed to develop a detailed mathematical model with high predictive ability for a real technological process.
3. Optimal process conditions for the discussed technological process of epoxy resins modification have been established with the developed mathematical model that includes chemical reaction mechanism, reactor hydrodynamics, heat and mass transfer phenomena. The proposed approach has been applied for solving the optimal control task for this industrial process with taking into account the acting disturbances – on the base of the detailed mathematical model developed through experimental study and kinetic modeling.
References
- Matzopoulos M. Dynamic process modeling: Combining models and experimental data to solve industrial problems. Process systems engineering: Dynamic process modeling. Edited by M.C. Georgiadis, J.R Banga and E.N Pistikopoulos (eds). Wiley-VCH Verlag, GmbH & Co., Germany. 2011; p. 7.
- Asprey SP, Macchietto S. Statistical tools for optimal dynamic model building. Comp Chem Eng. 2000; 24: 1261–1267.
- Schneider R, Sander F, Gorak A. Dynamic simulation of industrial reactive absorption processes. Chem Eng Process. 2003; 42: 955–964.
- Foss BA, Lohmann B, Marquardt W. A field study of the industrial modeling process. J Process Cont. 1998; 8: 325–338.
- Rolandi PA, Romagnoli JA. A framework for on-line full optimizing control of chemical processes. Proceedings of the ESCAPE15, Elsevier. The Netherlands. 2005; pp. 1315–1320.
- Luyben WL. Process modeling simulation and control for chemical engineers. 2nd edition, McGraw Hill, Singapore. 1995; pp. 17-124.
- Perry RH. Green D. Perry’s Chemical Engineers Handbook. 6th edition, McGraw Hill, Singapore, 1984.
- Kondili E, Pantelides CC, Sargent RWH. A general algorithm for short-term scheduling of batch operations – I. MILP formulation. Comp Chem Engg. 1993; 17(2): 211–227.
- Vlasov KP. Automatic control theory. Tutorial, Kharkov, Humanitarian center, Ukraine. 2006; p. 531.
- Lazarev TY, Martemyanov YF. The foundations of automatic control theory. Tutorial, 2nd revised and supplemented edition. Tambov, Russia. TSTU p. 352.
- Urevich EI. Automatic control theory. Tutorial, SPB, BCHV, 2007 p. 326.
- Pupkov KA, Egupov ND, Barkin AI, et al. Methods of classical and modern automatic control theory. Textbook, V.4, 2-nd revised and supplemented Edition. ?: ?S?U, 2004; p. 744.
- Benkovich ?S, Kolesov UB, Senichenkov UB. Practical modeling of dynamic systems. SPB: BCHV-Petersburg, Russia 2002; p. 464.
- Miroshnik IV. Automatic control theory. Non-linear and optimal systems. Tutorial, SPB: Piter, 2006; p. 272.
- Hsu JC, Meyer AU. Modern control principles and applications. McGraw-Hill book company, New York, USA. 1972 p. 544.
- Bemporad A, Morari M, Lawrence RN. Model predictive control. Mathworks, 2010; p. 205.
- Webster DC. Cyclic carbonate functional polymers and their applications. Progress in Organic Coatings. 2003; 47:77-86.
- Webster DC, Crain AL, Patil AO, et al. Functional polymers: Modern synthetic methods and novel structures. Am Chem Soc 1998; 704:303-320.
- Rosu D, Mustata F, Cascaval CN. Investigation of the curing reactions of some multifunctional epoxy resins using differential scanning calorimetry. Thermochim Acta. 2001; 370:105–110.
- Rosu D, Cascaval CN, Mustata F, et al. Cure kinetics of epoxy resins studied by non-isothermal DSC data. Thermochim Acta. 2002; 383:119–127.
- Sharikov FI, Sharikov IV. Kinetic study of modification of chlorine containing epoxy resins with using heat flux calorimetry. International Research Journal. 2014; 24:129-132.
- Sharikov YV, Beloglazov IN. Modeling of systems. Part 1. Edition of Saint-Petersburg Mining University. Saint-Petersburg, Russia. 2011; p. 108.
- Sharikov YV, Beloglazov IN. Modeling of systems. Part 2. Edition of Saint-Petersburg Mining University. Saint-Petersburg, Russia. 2012; p. 118.