Research Article - Biomedical Research (2017) Volume 28, Issue 20
An expert system for the prediction of stroke disease by different least squares support vector machines models
Mehmet Ediz Sarihan1* and Davut Hanbay2
1Department of Emergency Medicine, Faculty of Medicine, Inonu University, Malatya, Turkey
2Department of Computer Engineering, Faculty of Engineering, Inonu University, Malatya, Turkey
- *Corresponding Author:
- Mehmet Ediz Sarihan
Department of Emergency Medicine
Faculty of Medicine Inonu University Malatya, Turkey
Accepted date: September 26, 2017
Abstract
Objective: One of the important life-threatening ailment is stroke across the world. The current paper was performed to classify the outcome of stroke by using Least-Squares Support Vector Machines (LSSVMs) models.
Materials and Methods: The medical dataset related to stroke disease was achieved from the clinical database of the emergency medicine department. 28 predictors were recorded in raw dataset. For dimension reduction, correlations between input and target (stroke) variables were evaluated. Different LS-SVMs models were performed with radial basis function (RBF), linear and polynomial kernels. 5- fold cross-validation was used in composing stages to achieve the best model using all of the data. The accuracy and the Area under Receiver Operating Curve (AUC ROC) values were used for performance assessment.
Results: At first, feature selection stage was performed. 14 input variables were determined after this stage. Whole dataset was partitioned into 5 sub-datasets (D1, D2, D3, D4, D5) to use all data both training and testing. LS-SVMs models performance were evaluated by using 5-fold cross validation method. Accuracy and AUC values of the models were used as performance criteria. The best model performance was evaluated with LS-SVMs model using linear kernel. That model average accuracy was 86.6%. The best accuracy was evaluated with LS-SVM model using linear kernel on dataset D5 was 94%. As a consequence, the LS-SVMs model can be used for predicting the outcome of stroke.
Conclusion: The results point out that LS-SVMs with linear kernel have much more accuracy and AUC values for predicting stroke disease. The suggested LS-SVMs with linear kernel may produce beneficial prediction results related to stroke disease. In future studies, several data mining techniques may be tested and assembled for better classification performance of stroke disease.
Keywords
Data mining, Stroke disease, Least square support vector machines (LS-SVMs)
Introduction
Stroke is the significant reason of vascular behaviour and mentality disorderliness over the worldwide. In thriving countries, a shortage of information on the public health problem of stroke is present [1]. Stroke is an expanding illness and is an important reason of death worldwide following coronary heart disease and cancer ailment. Stroke frequently is the result of enhanced morbidity/mortality and lessened quality of life [2,3].
Data mining is a process of pattern discovery from a potentially large amount of data and is a multi-disciplinary topic that is conceived on the basis of logics in database systems. Examples of data mining techniques are Decision Trees, A priori Algorithm, Artificial Neural Networks (ANNs), Support Vector Machines (SVMs) and so on. Data mining can also be used in information technology evolving and subsequently branching off into sub-processes that include collecting data, creating database and management, analyzing data and finally interpreting data [4]. SVMs are one of the supervised machine learning (ML) approaches [5]. Since, then it is used widely in pattern recognition for regression and classification problems [6,7]. The LS-SVMs perform a classification by establishing a complex hyperplane optimally discriminating between two categories [6,7]. Kernel functions such as radial basis function (RBF), linear and polynomial are very powerful in mapping data into a larger dimensional domain and assist LS-SVMs to excellently separate data with very complex boundaries [8]. The LS version of the SVMs was described by Suykens and Vandewalle [9]. LS-SVMs are widely used in complex system studies [10].
In relation to the estimation of stroke, a study proposed SVMs in order to classify stroke thrombolysis, and the SVMs model yielded area under curve (AUC) of 0.744. The work showed that SVMs produced larger accuracy value than conventional, radiology-based techniques [11]. Another work investigated whether functional magnetic resonance imaging allowed classification of personal motor damage following stroke employing linear SVMs, and forty acute stroke people and 20 controls underwent resting-state functional magnetic resonance imaging for their goal. 82.6-87.6% accuracy was reported from the study [12]. Another study made a comparative analysis in the usage of SVMs with several kernel functions for stroke patients. The study investigated classifications accuracies of RBF, quadratic and polynomial kernel functions for different SVMs models [13]. Another study investigated SVMs for classifying the walking conditions of individuals following stroke, and reported that the predictive performance of SVMs model was higher than that of alternative data mining approaches utilizing RBF ANNs and ANNs [14].
In this work, an intelligent model is performed to predict the outcome of stroke disease using different LS-SVMs models. In section 2; the basic of the current study is described in details. In section 3; the application of the paper is explained. In section 4; conclusions are given.
Materials and Methods
Database
The current work was performed in the emergency medicine department, Turgut Ozal Medicine Center, Medical Faculty, Inonu University, Malatya, Turkey. Between January 2012 and January 2013, the medical enrollments of 104 individuals with stroke illness (patient group) and 104 healthy people (control group) were achieved from the database of the emergency medicine department. The recorded variables/factors were age (years), gender (1: female/2: male), educational status (1: primary school/2: middle school/3: high school/4: university/5: illiterate), marital status (MS; 1: married/2: single/3: widowed), application location for the emergency medicine service (LOC; 1: from home/ 2: from work/3: from any hospital), smoking status (SMO; 1: present/2: absent), coronary artery disease (1: present/2: absent), diabetes mellitus (1: present/2: absent), hypertension (1: present/2: absent), revascularization (REVAS; 1: angioplasty/2: stent/3: coronary bypass), hyperlipidemia (1: present/2: absent), electrocardiography (ECG; 1: present/2: absent), alcohol consumption (1: present/2: absent), congestive heart failure (CHF; 1: present/2: absent), systolic blood pressure (SBP; mmHg), diastolic blood pressure (DBP; mmHg), white blood cell (103/ML), hemoglobin (HB; g/dL), hematocrit (%), platelet (103/ML), glucose (mg/dL), blood urea nitrogen (mg/ dL), creatinine (mg/dL), sodium (Na; mmol/L), potassium (K; mmol/L), chlorine (CL; mmol/L), calcium (mg/dL), and international normalized ratio (INR; %). After correlation based feature selection approach [15], 14 of 28 input variables were used for predicting the outcome (target; 1: present/2: absent) of stroke disease. These variables were gender, age, MS, LOC, HT, REVAS, ECG, SMO, CHF, SBP, DBP, HB, K, and CL. A brief explanation of the database used in this study is shown in Table 1. The predictors included in this study are similar with the risk factors of stroke disease reported by other clinical research articles [16-19].
| Target | Gender | Age | MS | LOC | HT | REVAS | ECG | SMO | CHF | SBP | DBP | HB | K | CL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 62 | 1 | 3 | 2 | 2 | 2 | 2 | 2 | 174 | 85 | 13 | 4 | 100 |
| 1 | 2 | 63 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 180 | 100 | 16 | 4 | 107 |
| 1 | 2 | 80 | 1 | 3 | 1 | 2 | 2 | 2 | 1 | 190 | 105 | 16 | 4 | 100 |
| 1 | 1 | 78 | 1 | 3 | 1 | 2 | 2 | 2 | 1 | 190 | 108 | 13 | 5 | 108 |
| 1 | 2 | 77 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 199 | 100 | 16 | 5 | 109 |
| 1 | 2 | 58 | 3 | 3 | 2 | 2 | 2 | 1 | 2 | 107 | 70 | 15 | 4 | 99 |
| 1 | 2 | 50 | 1 | 3 | 2 | 2 | 2 | 1 | 2 | 188 | 108 | 15 | 5 | 101 |
| 1 | 2 | 81 | 1 | 3 | 2 | 2 | 2 | 2 | 2 | 129 | 74 | 12 | 4 | 111 |
| 1 | 1 | 76 | 3 | 3 | 1 | 2 | 2 | 2 | 2 | 185 | 98 | 14 | 4 | 106 |
| 1 | 2 | 79 | 1 | 3 | 2 | 2 | 2 | 1 | 2 | 166 | 98 | 13 | 4 | 112 |
| 1 | 2 | 76 | 1 | 3 | 1 | 1 | 2 | 1 | 1 | 185 | 85 | 15 | 5 | 109 |
| 1 | 1 | 74 | 3 | 1 | 1 | 2 | 2 | 2 | 1 | 220 | 92 | 13 | 4 | 104 |
| 1 | 2 | 57 | 1 | 3 | 2 | 2 | 2 | 1 | 2 | 120 | 76 | 11 | 4 | 109 |
| 2 | 2 | 25 | 2 | 1 | 2 | 2 | 2 | 1 | 2 | 125 | 76 | 16 | 4 | 108 |
| 2 | 1 | 37 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 153 | 116 | 12 | 5 | 108 |
| 2 | 2 | 35 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 111 | 70 | 14 | 5 | 109 |
| 2 | 2 | 29 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 100 | 63 | 14 | 5 | 102 |
| 2 | 1 | 89 | 3 | 1 | 1 | 2 | 2 | 2 | 2 | 159 | 96 | 11 | 4 | 110 |
| 2 | 2 | 25 | 2 | 1 | 2 | 2 | 2 | 1 | 2 | 111 | 59 | 15 | 4 | 105 |
| 2 | 1 | 37 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 162 | 94 | 12 | 5 | 109 |
| 2 | 1 | 21 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 116 | 77 | 13 | 4 | 109 |
| 2 | 1 | 23 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 101 | 59 | 11 | 4 | 107 |
| 2 | 1 | 18 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 117 | 83 | 14 | 4 | 111 |
| 2 | 1 | 65 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 154 | 67 | 9 | 4 | 103 |
| 2 | 1 | 60 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 168 | 113 | 10 | 4 | 114 |
| 2 | 1 | 32 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 129 | 89 | 11 | 4 | 110 |
| 2 | 2 | 82 | 1 | 3 | 1 | 1 | 2 | 1 | 1 | 136 | 100 | 9 | 7 | 114 |
| 2 | 1 | 37 | 1 | 2 | 2 | 1 | 2 | 1 | 1 | 134 | 69 | 15 | 5 | 109 |
| 2 | 2 | 70 | 1 | 3 | 2 | 2 | 2 | 2 | 2 | 92 | 60 | 13 | 4 | 103 |
| 2 | 1 | 68 | 1 | 3 | 2 | 2 | 1 | 2 | 2 | 144 | 90 | 13 | 5 | 108 |
Table 1. A brief explanation of the database used in this study.
Least square support vector machines (LS-SVMs)
SVMs are one of the supervised ML techniques developed by Vapnik et al. at AT&T Bell Laboratories in 1995 [20]. It can be used for both classification and regression tasks in any discipline. The SVMs are based on the principle of structural risk minimization [20,21].
If a given training set 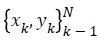 with input data xk Rn and
output data yk R with class labels yk {-1, +1} and linear
classifier
with input data xk Rn and
output data yk R with class labels yk {-1, +1} and linear
classifier 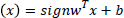 (1)
(1)
If two classes can be separable then
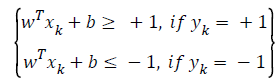 (2)
(2)
These two equations can be combined and reduced to one equation as in Eq. 3.
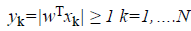 (3)
(3)
SVMs subject is a concept of convex optimization theory. At first, the problem is stated as a constrained optimization problem. Then Lagrangian is formulated and the conditions for optimality are determined; finally, the problem is solved in the dual space of Lagrange multipliers with Eq. 4.
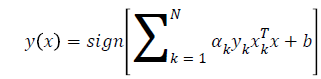 (4)
(4)
Cortes & Vapnik were extended this linear SVMs classifier to non-separable case. It is done by adding slack variable in the problem formulation as in Eq. 5.
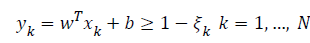 (5)
(5)
The SVMs have not been used only for linear function estimation; but also they have been used for nonlinear function estimation too.
The least square type of the SVMs methods were proposed Suykens and Vandewalle [21]. In the LS-SVMs methods equality type constraints are considered instead of inequalities [22]. This reformulation greatly simplifies a problem such that the LS-SVMs solution follows directly from solving a sequence of linear formulas rather than from a convex quadratic program. The LS-SVMs classifier, in the primal space can be described by Eq. 6.
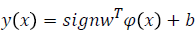 (6)
(6)
Where ϕ(.) map from input space to feature space and b is a real constant. For nonlinear classification, the LS-SVM classifier in the dual space it takes the form
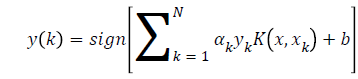 (7)
(7)
For function estimation, the LS-SVM model can be described by Eq. 8.
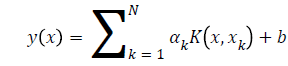 (8)
(8)
There are many types of kernels used with SVMs and LSSVMs: the most known of them are linear, polynomial and radial basic function kernels. These kernels are tabulated in Table 2.
| Kernels Types | Equations |
|---|---|
| Linear | 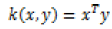 |
| Polynomial | 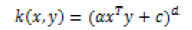 |
| RBF | 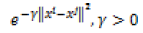 |
Table 2. Kernel Types of LS-SVMs.
The Linear kernel is the simplest kernel function. It is given by the inner product <x,y> plus an optional constant c. When RBF kernels are used, two tuning parameters (γ,α) are added. Where Φ(.) map from input space to feature space and b is a real constant, K(.) is kernel function, γ is regularization constant, and σ is width of RBF kernel. The Polynomial kernel is a nonstationary kernel. Polynomial kernels are well suited for problems where all the training data are normalized [3].
Results
This study was launched to estimate the outcome of stroke disease using several LS-SVMs models. After correlation based feature selection, the aforementioned variables were used for predicting the outcome of stroke disease. Different LS-SVMs models with RBF, Linear and Polynomial kernels were composed. 5-fold cross-validation was used to evaluate the models performance by using all data. The instances having empty values were ignored too. All program codes were written in MATLAB.
In 5-fold cross-validation, the stroke database was partitioned randomly into 5 sub-datasets, and training and testing were repeated for 5 times. Average accuracy of 5 models was accepted as model accuracy. To gauge the classifiers’ performance, accuracy and area under receiver operating characteristic curve (ROC) were considered as performance metrics.
At first, accuracy and ROC values of LS-SVMs models were evaluated. Averaged accuracy percentages were 85.6% for LSSVMs with RBF kernel, 86.6% for LS-SVMs with linear kernel, and 74.4% for LS-SVMs with polynomial kernel. As a consequence, the best LS-SVMs model was obtained with linear kernel.
Table 3 presents the results of LS-SVMs models. Based on the Table 3, the highest average accuracy is 86.6% for LS-SVM with linear kernels, and the largest average AUC is 0.9729 for LS-SVM.
| Testing Dataset | Accuracy for RBF kernel (%) | Accuracy for linear kernel (%) | Accuracy for polynomial kernel (%) | AUC for RBF kernel | AUC for linear kernel | AUC for polynomial kernel |
|---|---|---|---|---|---|---|
| D1 | 86 | 86 | 78 | 0.8591 | 0.9732 | 0.775 |
| D2 | 86 | 86 | 69 | 0.8875 | 0.9732 | 0.6905 |
| D3 | 81 | 78 | 69 | 0.8372 | 0.9881 | 0.694 |
| D4 | 86 | 89 | 78 | 0.881 | 0.9654 | 0.8052 |
| D5 | 89 | 94 | 78 | 0.9 | 0.9648 | 0.775 |
| Average | 85.6 | 86.6 | 74.4 | 0.873 | 0.9729 | 0.7479 |
Table 3. The results of LS-SVMs models using different kernels.
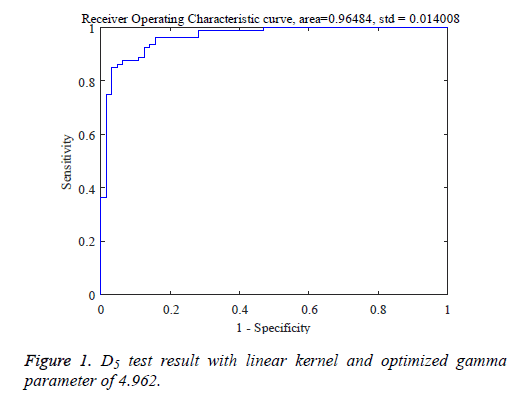
Simplex cost function optimization routine was used for tuning the LS-SVM kernel parameters. Sample ROC graphic for D5 is shown in Figure 1 with linear kernel and optimized gamma parameter of 4.962.
Conclusion
In the first stage of the current study, we investigated the possible use of LS-SVMs models by different kernels in the prediction of stroke. In the second stage, performance of LSSVMs models was compared for predicting the outcome of stroke and compared based on the accuracy rates and AUC values. The obtained results of this work indicated that LSSVMs with linear kernel had more accuracy and AUC for the prediction stroke disease.
The current study demonstrated the possible use of LS-SVMs models by different kernels in the prediction of stroke considering a small set of clinical variables. When the suggested model includes larger data sets, containing many other demographical and clinical variables associated with stroke disease, the prediction performance may be higher.
The results point out that LS-SVMs with linear kernel have much more accuracy and AUC values as compared with other LS-SVMs models in predicting stroke disease. The suggested LS-SVMs with linear kernel may produce beneficial prediction results related to stroke disease. In future studies, several data mining techniques may be combined for better classification performance of stroke disease.
References
- Arauz A, Rodriguez-Agudelo Y, Sosa AL, Chavez M, Paz F, Gonzalez M, Coral J, Díaz-Olavarrieta C, Román GC. Vascular Cognitive Disorders and Depression After First-Ever Stroke: The Fogarty-Mexico Stroke Cohort. Cerebrovasc Dis 2014; 38: 284-289.
- Ogbera AO, Oshinaike OO, Dada O, Brodie-Mends A, Ekpebegh C. Glucose and lipid assessment in patients with acute stroke. Int Arch Med 2014; 7: 45.
- Colak C, Karaman E, Turtay MG. Application of knowledge discovery process on the prediction of stroke. Comput Methods Programs Biomed 2015; 119: 181-185.
- Paramasivam V, Yee TS, Dhillon SK, Sidhu AS. A methodological review of data mining techniques in predictive medicine: An application in hemodynamic prediction for abdominal aortic aneurysm disease. Biocybern Biomed Eng 2014.
- Cortes C, Vapnik V. Support vector machine. Mach Learn 1995; 20: 273-297.
- Hariharan M, Polat K, Sindhu R. A new hybrid intelligent system for accurate detection of Parkinson's disease. Comput Methods Programs Biomed 2014; 113: 904-913.
- Li Y, Wen PP. Clustering technique-based least square support vector machine for EEG signal classification. Comput Meth Prog Bio 2011; 104: 358-372.
- Hanbay D. An expert system based on least square support vector machines for diagnosis of the valvular heart disease. Expert Syst Appl 2009; 36: 4232-4238.
- Van Gestel T, Suykens JA, Lanckriet G, Lambrechts A, De Moor B, Vandewalle J. Bayesian framework for least-squares support vector machine classifiers, gaussian processes, and kernel Fisher discriminant analysis. Neural Comput 2002; 14: 1115-1147.
- Sengur A. Multiclass least-squares support vector machines for analog modulation classification. Expert Syst Appl 2009; 36: 6681-6685.
- Yu W, Liu T, Valdez R, Gwinn M, Khoury MJ. Application of support vector machine modeling for prediction of common diseases: the case of diabetes and pre-diabetes. BMC Med Inform Decis. 2010; 10: 16.
- Bentley P, Ganesalingam J, Jones ALC, Mahady K, Epton S, Rinne P, Sharma P, Halse O, Mehta A, Rueckert D. Prediction of stroke thrombolysis outcome using CT brain machine learning. Neuroimage-Clin 2014; 4: 635-640.
- Farid N, Elbagoury B, Roushdy M, Salem AB. A Comparative Analysis for Support Vector Machines For Stroke Patients. Rec Adv Inf Sci 2013; 71-76.
- Lau H, Tong K, Zhu H. Support vector machine for classification of walking conditions of persons after stroke with dropped foot. Hum Movement Sci 2009; 28: 504-514.
- Michalak K, Kwasnicka H. Correlation-based feature selection strategy in classification problems. Int J Appl Math Comp 2006; 16: 503-511.
- Wolf PA. Risk factors for stroke. Stroke 1985; 16: 359-360.
- Go AS, Hylek EM, Phillips KA, Chang Y, Henault LE, Selby JV, Singer DE. Prevalence of diagnosed atrial fibrillation in adults: national implications for rhythm management and stroke prevention: the AnTicoagulation and Risk Factors in Atrial Fibrillation (ATRIA) Study. JAMA 2001; 285: 2370-2375.
- Welin L, Svärdsudd K, Wilhelmsen L, Larsson B, Tibblin G. Analysis of risk factors for stroke in a cohort of men born in 1913. N Engl J Med 1987; 317: 521-526.
- Boysen G, Nyboe J, Appleyard M, Sørensen PS, Boas J, Somnier F, Jensen G, Schnohr P. Stroke incidence and risk factors for stroke in Copenhagen, Denmark. Stroke 1988; 19: 1345-1353.
- Cortes C, Vapnik V. Support-vector networks. Mach Learn 1995; 20: 273-297.
- Suykens JA, Vandewalle J. Least squares support vector machine classifiers. Neural Process Lett 1999; 9: 293-300.
- Übeyli ED. Least squares support vector machine employing model-based methods coefficients for analysis of EEG signals. Expert Syst Appl 2010; 37: 233-239.