Case Report - Biomedical Research (2017) Volume 28, Issue 12
A case study of fault-tolerant biological systems with MRI images
Elamaran V*, Narasimhan K, Balaji VS, Chandrasekar M and Har Narayan Upadhyay
School of EEE, SASTRA University, Thanjavur, India
Accepted on April 10, 2017
Abstract
Biological systems which store medical images should have high reliability in real time. This study explores the implementation of fault-tolerant systems using Magnetic Resonance Imaging (MRI) scan images with image enhancement algorithms. If some of the pixels in the image become faulty or erroneous, the accuracy of the information is lost and hence the necessity of fault-tolerant systems would be more important. The high-pass filters are used here to obtain edges in the images with hardware redundancy techniques like Triple Modular Redundancy (TMR) which are used to tolerate one single event error. The 5-MR methods are also explored to tolerate two errors. This is a kind of case study demonstrates with producing high frequency content even from the blurred input image. These biological systems are implemented on Altera EP4CE115F29C7 FPGA device using Quartus II synthesis software tool. A 7 × 7 high-pass filter consumes more number of logic elements (878), registers (821) and memory bits (10486) than 2 × 2, 3 × 3 and 5 × 5 filters.
Keywords
MRI images, Fault-tolerant, Image enhancement, Reliability.
Introduction
The physical defect and a flaw or imperfection in software or hardware can create fault in the system. In microelectronic circuits, these faults may happen due to open in a wire, short between wires or a break in components; in software, these faults would occur due to infinite program loop. Also if there is an incorrect algorithm or a poorly specified requirement, the system will face faults. If the system design is poor or has program coding mistakes, the faults will degrade the system performance.
In the field of medical electronics, the diagnostic tools play a vital role in detecting abnormal changes in organs and tissues early. The most popular diagnostic tools are MRI, Computer Tomography (CT), and Position Emission Tomography (PET) [1]. The MRI scan images are very often used for the clinical diagnosis because of the ability to obtain high quality picture [2]. In general, the steps involved to obtain MRI scan image are simple. The person is placed on a magnet and the radio waves are sent in. Then the radio signals are switched off so that the person’s body emits the signal. This signal is received appropriately and used to obtain the picture [3]. Here, the property of Nuclear Magnetic Resonance (NMR) is used to obtain the image nuclei atoms inside the body. The magnetization of atoms in the human body is aligned by the strong magnetic field which is from an MRI machine.
The ability of a system to obtain the correct output even though there are faults in a system is known as “fault tolerance”. If the system fails or fault occurs, it can’t function correctly and can’t meet the requirements [4]. In the hardware, the faults can happen as a broken connection. The software faults would occur due to the bug in the program [5]. The ability of a system to serve its intended level of service to the customers is known as “dependability”.
The redundancy technique is a very common method to achieve the fault tolerance in a system by means of duplicated hardware components, attaching parity bits at the end of information and series of programs to check the correctness of the result [6]. The applications of fault tolerance are classified as safety-critical, mission-critical and business-critical. Loss of human lives or environmental disaster should be avoided in the case of safety-critical applications like in pacemakers and aircraft control systems [7]. We use mission-critical application for the launch of either Satellite or Spacecraft. Automated trading system with stock exchange is a good example of business-critical application where the business should operate continuously without any problem [8].
Materials and Methods
N-modular redundancy
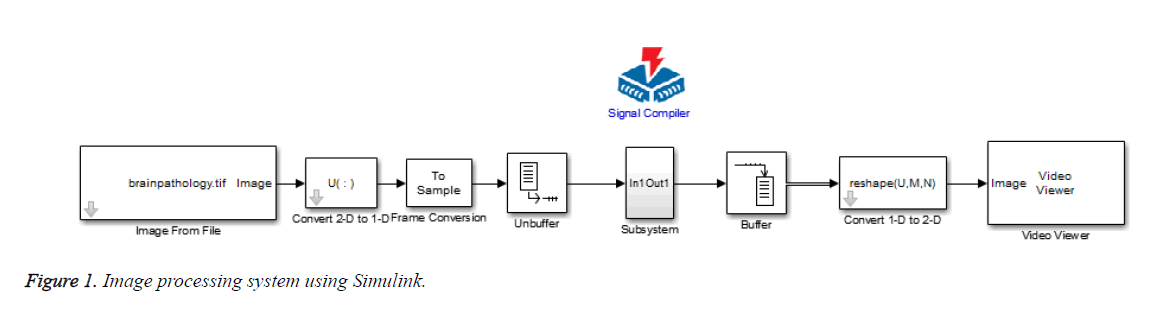
This study demonstrates the hard ware redundancy techniques to improve the reliability of system with inputs as MRI scan image. In the TMR approach, the original module is replicated two times as three modules are operated in the system.
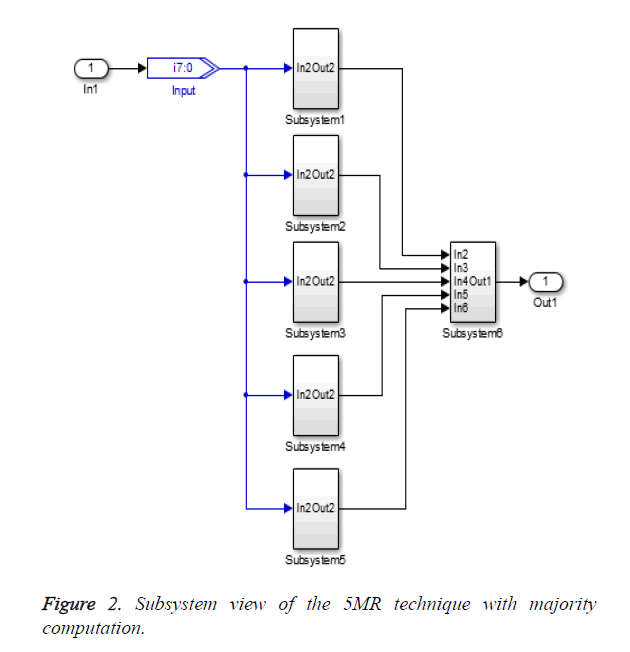
If one module fails, the majority is computed using the voting circuit and thus obtain the correct response. This method can tolerate one error at a time. That is, if any soft error happens in a module which is masked by the voting circuit. In the case of N-Modular Redundancy (NMR) approach, (N-1) copies of the actual module are replicated and the fault free result is obtained using an appropriate voting circuit [9]. The 5-MR approach is demonstrated in detail in this study to tolerate 2 errors. The overall system and the 5-MR approach are depicted in Figures 1 and 2 respectively.
The majority computation is done as follows,
Out=ABC+ABD+ABE+ACD+ACE+ADE+BCD+BCE+BDE +CDE → (1)
Where A, B, C, D and E are the five modules in a system. If any two systems fail, this Out will produce the fault free response by obtaining the majority as an output. This study exemplifies two application examples to carry out this hardware redundancy work.
Application example 1: edge detection
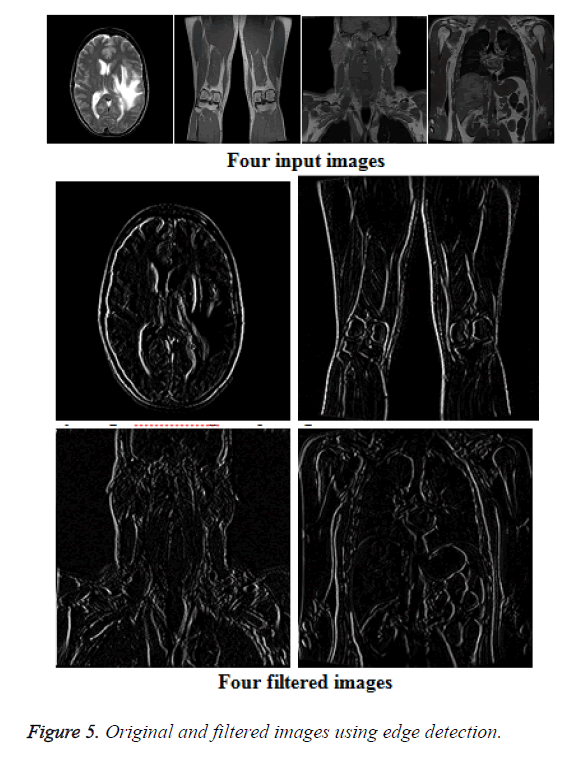
Edge detection is a popular technique in almost all field of imaging applications to obtain the high frequency data in a picture [10,11]. The 2 × 2, 3 × 3, 5 × 5 and 7 × 7 high-pass filters are used for the system utility comparison with FPGA target board. These filters are shown as follows,
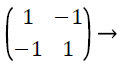 (2)
(2)
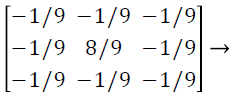 (3)
(3)
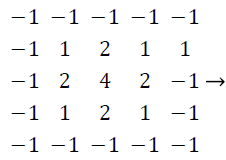 (4)
(4)
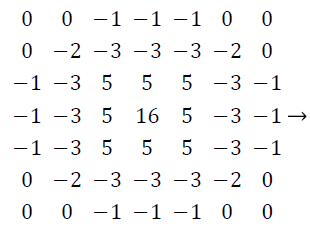 (5)
(5)
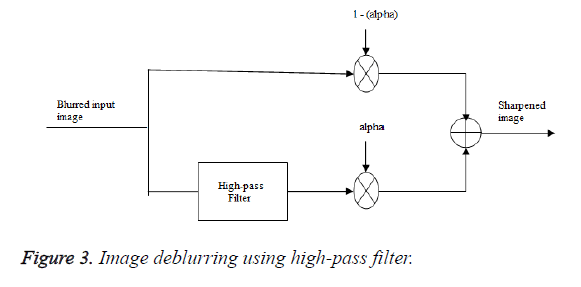
Application example 2: image deblurring
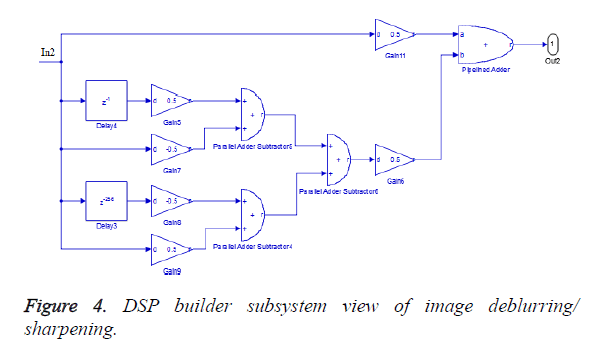
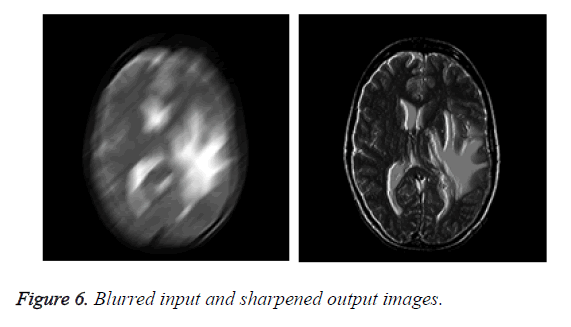
If the image data is blurred, image deblurring (sharpening) plays a vital role to retrieve the actual content from a picture. This method is shown in Figure 3. The blurred input is applied here to the high-pass filter to sharpen the edges. The alpha value is taken as 0.5 and this method is implemented using Altera DSP builder DSP blocks as in Figure 4.
Results and Discussion
Edge detection
The high frequency content information is obtained using high-pass filters which become edges of the MRI scan data. The input MRI images and the corresponding filtered images are shown in Figure 5. Here the four MRI scan test images (256 × 256) are used, namely head subset, thigh subset, thorax subset and abdomen subset which are the specimens from the visible human male.
Deblurring
The output image obtained from the deblurring method is shown in Figure 6. This helps to diagnose in a better way with MRI scan images.
Results and discussion
The edge detection and deblurring are the two application examples which are implemented on an Altera FPGA device EP4CE115F29C7 and the resource utilization summary report is obtained in Table 1. As expected, the 7 × 7 high-pass filter occupies more number of logic elements (878), registers (821) and memory bits (10,486) than other filters. Also, it consumes more power dissipation (156.16 mW), lower performance (58.11 MHz), and higher critical path delay (11.816 ns) than others filters. The deblurring system has 355 logic elements, 328 registers, 4292 memory bits, 10.76 ns delay, 71.12 MHz performance, and 149.12 mW power dissipation respectively.
| Method | Logic elements | Registers | Memory bits | Critical path delay (ns) | Performance (MHz) | Power dissipation (mW) |
|---|---|---|---|---|---|---|
| 2 2 high pass filter | 83 | 72 | 1764 | 7.678 | 114.63 | 137.46 |
| 3 3 high pass filter | 240 | 207 | 3525 | 9.855 | 72.44 | 144.98 |
| 5 5 high pass filter | 497 | 464 | 6993 | 11.220 | 67.76 | 153.34 |
| 7 7 high pass filter | 878 | 821 | 10486 | 11.816 | 58.11 | 156.16 |
| Deblurring | 355 | 328 | 4292 | 10.76 | 71.12 | 149.12 |
Table 1. Simulation results with Altera EP4CE115F29C7 FPGA resource utilization summary.
Reliability analysis
Let RA, RB, and RC are the reliabilities of modules A, B, and C respectively in order to evaluate the reliability of a TMR configuration with a perfect voter. If all the modules function correctly, then the reliability of a TMR system is “RARBRC”. If the module A fails, it becomes “(1-RA) RBRC”; if the module B fails it becomes “RA (1-RB) RC” and if the module C fails, it becomes “RARB (1-RC)”. These events are mutually exclusive and hence the overall TMR system reliability can be expressed as:
RTMR=Probability of no failures+Probability of failure in module A+Probability of failure in module B+Probability of failure in module C=RARBRC+(1–RA) RBRC+RA (1-RB) RC +RARB (1-RC)=R3+3 (1-R) R2=3R2–2R3 (if RA=RB=RC=R) → (6)
Let RA, RB, RC, RD, and RE are the reliabilities of modules A, B, C, D, and E respectively to evaluate the reliability of a 5- MR configuration with a perfect voter. If all the modules function correctly, then the reliability of a TMR system is “RARBRCRDRE”. If the modules A and B fail, it becomes “(1-RA) (1-RB) RCRDRE”; if the modules A and C fail it becomes “(1-RA) RB (1-RC) RDRE” and so on. Again these events are mutually exclusive and hence the overall 5MR system reliability can be expressed as:
R5MR=Probability of no failures+Probability of failures in module A and B+Probability of failures in module A and C +Probability of failures in module A and D +. . .+ Probability of failures in module D and E
=RARBRCRDRE+(1-RA) (1-RB) RCRDRE+(1-RA) RB (1-RC) RD RE+...+RARBRC (1-RD) (1-RE)
=10R3 (1–R)2+5R4 (1-R)+R5 (if RA=RB=RC=RD=RE=R) → (7)
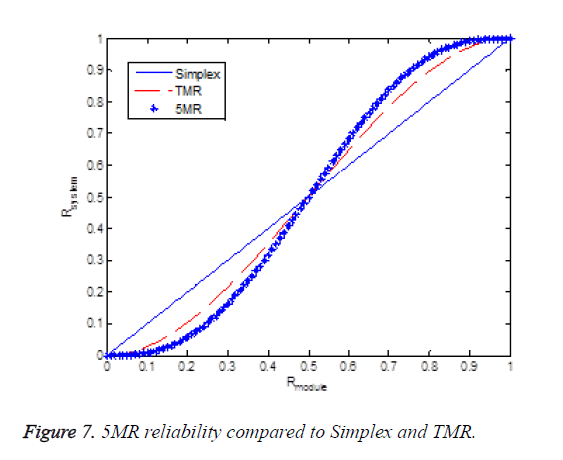
The Figure 7 shows the reliability comparison among the simplex, a TMR system, and a 5-MR system. It shows that the reliability of a 5-MR system is better if the reliability of a module is more than 0.5. For example, if the reliability of a module is R=0.7, then Rsimplex=0.7, RTMR=0.7840, and R5MR=0.8369.
Conclusion
The objective of the fault tolerance is to increase the dependability of any system. In this study, it is achieved in terms of hard ware redundancy with two application examples such as edge detection and deblurring with MRI scan images. This study can be further extended to information redundancy where the data is embedded with parity bits to detect the error and for correction we use Hamming codes. Also, this work can further be taken to other image processing operations like point processing, morphological processing, image restoration, image classification, and image segmentation problems.
Acknowledgment
We thank SASTRA University for providing financial support for this research work under the Research and Modernization fund-R&M/0034/SEEE-014/2013-14. We also sincerely thank the reviewers whose thoughtful comments helped to improve our article substantially.
References
- Adeline Sneha J, Akshaya PS, Indira KP, Amala Rani V. Emerging technology based on adaptive filtering algorithm for MRI Scans. Res J Pharm Biol Chem Sci 2015; 6: 539-544.
- Moldovanu S, Moraru L, Biswas A. Edge-based structural similarity analysis in brain MRI images. J Med Imaging Health Inform 2016; 6: 539-546.
- Kalavathi P, Prasath VB. Methods on Skull Stripping of MRI Head Scan Images-a Review. J Digit Imaging 2016; 29: 365-379.
- Elamaran V, Har Narayan Upadhyay. CMOS VLSI design of low power SRAM cell architectures with new TMR: A layout approach. Asian J Sci Res 2015; 8: 466-477.
- Elamaran V, Har Narayan U. CMOS VLSI design of low power SRAM cell architectures with new TMR: A layout approach. Asian J Sci Res 2015; 8: 466-477.
- Kshirsagar KV, Patrikar RM. Design of a novel fault-tolerant voter circuit for TMR implementation to improve reliability in digital circuits. Microelect Reliab 2009; 49: 1573-1577.
- Elamaran V, Hemavathy R, Jayapriya D, Har Narayan Upadhyay. Majority function computation using different voter circuits-a comparative study. Int J Pharm Technol 2015; 7: 9764-9773.
- Balasubramanian P, Maskell DL. A distributed minority and majority voting based redundancy scheme. Microelectr Reliab 2015; 55: 1373-1378.
- Balasubramanian P. ASIC-based design of NMR system health monitor for mission/safety-critical applications. Springer Plus 2016; 5: 1-16.
- Elamaran V, Praveen A, Reddy MS, Aditya LV, Suman K. FPGA implementation of spatial image filters using Xilinx system generator. Proc Eng 2012; 38: 2244-2249.
- Elamaran V, Rajkumar G. FPGA implementation of point processes using xilinx system generator. J Theor Appl Inform Technol 2012; 41: 201-206.